《机器学习实战》书中第5章讲的是逻辑回归（Logistic回归）。

满怀鸡冻放开书本，结果读了好几遍都没弄明白其原理。弄不懂逻辑回归实现代码为什么要那么写！

至少我已经先学过斯坦福大学教授Andrew Ng讲所的机器学习中的线性回归。还是看不明白书中梯度上升部分的代码。（拍照技术一般，拍纸质书比较模糊。为了方便指出位置，找了该书的pdf文件，截图如下。）

最后，通过大量搜索和学习。该部分涉及到导数、最大似然估计、梯度上升等知识。

下面一一给大家分享我学习的成果。

1、什么是逻辑回归（Logistic回归）

逻辑回归也是一种分类算法。一般用于医疗、天气预报等。

例如观测到两组数据多个样本成像如下：

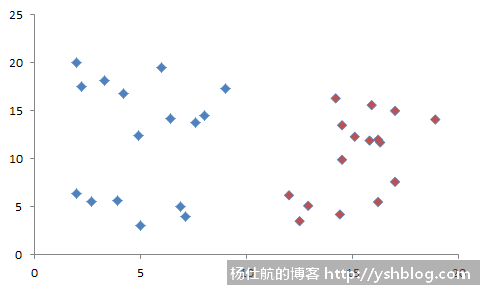
可以看出，蓝色和红色的数据点扎堆。那么，我是不是可以找到一条边界线。

这条边界线划分两种分类，在边界线左边是蓝色分类；在边界线右边是红色分类。

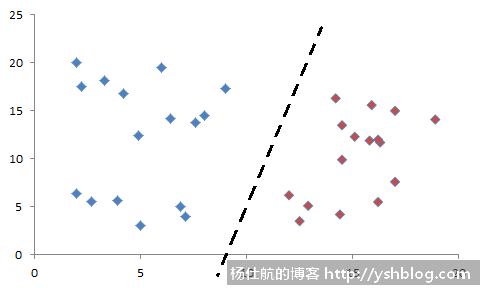
这条边界线也叫决策线。寻找这条边界线是线性回归问题。

根据输入特征的个数（输入数据种类个数），可写成如下的线性方程：

z = θ₀X₀+θ₁X₁+θ₂X₂+...+θ_nX_n , 其中X₀=1

该部分若不明白，可以看看Andrew Ng的公开课：监督学习应用.梯度下降。前半部分就传授了什么是线性回归，即线性方程。

假如输入变量只有1个，就是我们熟悉的一元线性方程 y = ax+b。

为了方便书写和计算，可写成y = θ₁X₁+θ₀X₀，并令X₀=1。

若你懂得求和符号的话，z方程可以写成如下：

也可以简写成 z = θ^TX

2、利用Sigmoid函数分类

那么，我们求得这个z只是边界线上的点，这个点如何和分类结果对应？

也就是说，我们应当如何通过边界线进行分类。这里需要利用Sigmoid函数，也叫S型函数。

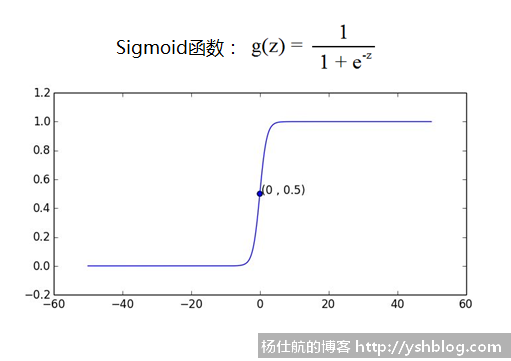
当z=0时，g(z)=0.5；z越小，g(z)越接近0；z越大，g(z)越接近1。

通过该特性，即是边界线的限制条件，又可以给数据提供划分分类方法。

通过g(z)和0.5对比，划分分类。

3、如何拟合线性方程（边界线）

这里利用最大似然估计和梯度上升的方法去拟合线性方程，找到最佳的θ系数。

当然，你也可以尝试最小二乘法和梯度下降的方法。(上面Andrew Ng教授的视频有讲)

因为，X是我们输入的数据，无需理会，可以将其当作变量。系数θ才是我们真正想要找的，这样才能确定线性方程。

最大似然估计需要通过似然函数求得。先了解一下什么是似然。

似然和概率相反的过程：

1）概率是已知参数或条件，预测或观测可能发生的结果；

2）似然是已知某些观测到的结果，估计相关的参数或条件。

例如，抛1次硬币，结果是正面的概率为0.5。

那么，反过来。不知道抛了几次硬币，正面的概率为0.5。估计一下抛了多少次硬币。利用结果反过来求参数和我们现在在处理的线性回归思路一样的。我们已知一些数据，求边界线的参数(θ₁，θ₂，...， θ_n)。

理解似然之后，继续加深。因为估计抛硬币的次数很有多种情况。抛2次硬币甚至3次硬币，正面向上的观测结果也可能出现0.5的概率，只是概率相对比较小。

所以，我们要求解最合理的似然估计参数，就是对应求解概率最大的情况，即最大似然估计。

相关知识可看该链接：http://baike.baidu.com/item/似然函数

那么，我们如何求得最大似然估计呢？

这里需要导数的知识，不懂该方面知识可以看麻省理工：单变量微积分公开课第1~7集。我恶补一番导数的知识才研究明白后面的推导过程。

导数是体现变化率。当变化率为0时，说明该位置是顶点位置。（局部最大值或最小值）

对于一元方程，某一点的导数最直观的体现是该点切线的斜率。

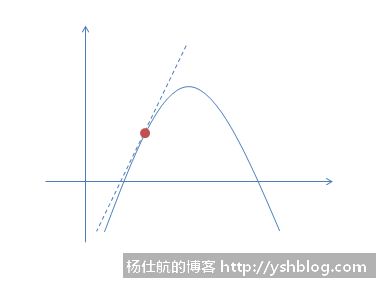
回想一下抛物线，一元二次方程。最大值或最小值的导数为0，即切线斜率为0。

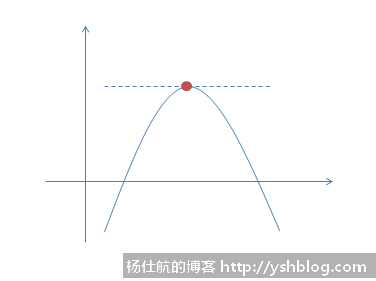
但对于一个似然函数，通常有很多个参数待确定。不能直接求得导数为0的点。

这里采用梯度上升的方法，去拟合结果。

首先，在似然函数上随机初始化一个点，并求得其导数（切线的斜率）。该导数就告知梯度上升的方向。

我们将数据点往导数（斜率）的方向挪动小小一步（根据导数的线性近似，可看上面麻省理工视频第8集）。

挪动之后，再重新计算一次新位置的导数，继续重复挪动，直到导数为0。即可认为到达最大值。

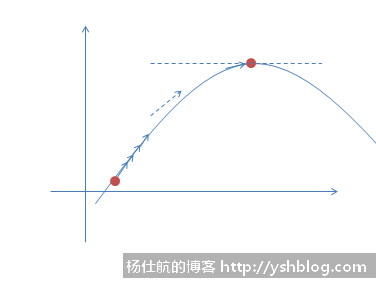
这是一个反复迭代的过程。表达式如下：

θ_j := θ_j + α*θ_j′ 

其中，:=表示右边的值赋值给左边，α代表每次挪动的步长，θ_j′ 是该点对应的导数。

实际编写代码实现功能的时候，不会判断导数是否为0。

因为每次计算都要判断，效率过低。通常做法是固定迭代次数。

固定迭代次数可能导致过度拟合或者拟合不足的情况。后面还有其他方法优化。

4、逻辑回归的最大似然估计

了解所需要的知识后，推导逻辑回归边界线参数的最大似然函数求解过程。也是《机器学习实战》书中缺少的关键部分。

设 y = h_θ(x) = g(z) = g(θ^Tx)。g(z)是Sigmoid函数，可以划分两种分类：0和1。

那么，y=1和y=0的概率可以假设为

P(y=1 | x;θ) = h_θ(x) 

P(y=0 | x;θ) = 1 - h_θ(x) 

注意，P(y=1 | x;θ)非条件概率，是似然估计的表示方式。这两个可以合并为如下表达式：

P(y | x;θ) = h_θ(x)^y(1 - h_θ(x))^(1-y)

假如我们观测了m个样本，这些样本都是独立分布。可形成对应的似然函数为：

L(θ)为θ的参数的分布函数。也是我们梯度递增所需要的导数的原函数。

但要求解该函数的导数困难极大，而且求解所需计算量大。通常，我们会取该似然函数的自然对数。将乘法运算转化为加法运算简化计算。

由于对数函数是单调递增函数，不会改变原来函数最大值的位置。即其和L(θ)在同样的位置都有对应的最大值。所以我们一般会用自然对数似然函数代替原似然函数。

那么，自然对数似然函数为：

为了简化计算，我们可以假设只有一个样本(x, y)。因为每一项求导结果都一样。

对θ求偏导，求导过程如下：

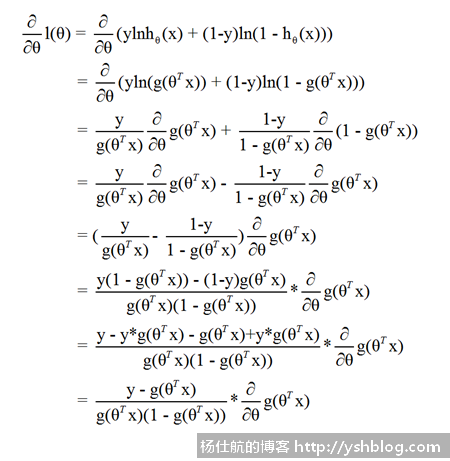
第1步到第2步是因为 y = h_θ(x) = g(z) = g(θ^Tx)。

这里可能有疑问的是第3行，使用到求导的链式法则。可以看麻省理工：单变量微积分的课程。

假设 t = g(θ^Tx)，即

自然对数的ln(t)导数是t。第2步，分子分母同时乘以偏导t，不影响结果。

上面计算卡在了，还需要计算g(θ^Tx)的导数。g(θ^Tx)=g(z)，求解如下：

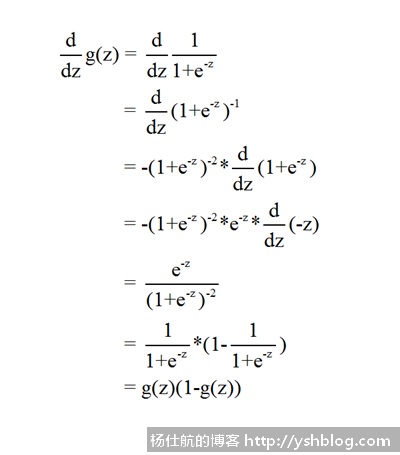
这里面也运用到了链式法则，以及指数的导数公式。

结果为g(z)’=g(z)(1-g(z))。

那么，上面的自然对数似然函数的导数继续求解。

求得，梯度上升的迭代规则为θ_j := θ_j + α*(y⁽ⁱ⁾-h_θ(x⁽ⁱ⁾))*x_j⁽ⁱ⁾

这里x_j⁽ⁱ⁾还涉及到多元求导。同时多个样本求导，每个参数上的样本都对应x特征。所以这里需要同时计算多个样本的乘积结果，再求和得到自然对数似然函数的导数。

接下来，可以利用该迭代规则计算θ参数。

5、Python代码实现逻辑回归分类

相关素材文件可以打开Github中的machinelearninginaction项目。

其中，样本放在testSet.txt文件中。一共100个行，每行前两个为输入的特征值，最后一个为分类。

读取该文件的代码如下：

#coding:utf-8
import numpy as np

#获取训练集
def load_dataset(filename='testSet.txt'):
    dataset = []
    labels = []
    with open(filename, 'r') as f:
        line = f.readline()
        while line != '':
            data = line.strip().split()
            dataset.append([1., float(data[0]), float(data[1])])
            labels.append(int(data[2]))
            line = f.readline()

    return dataset, labels

和书中不同，我将读取文件的代码用while循环代替for循环。

不直接用readlines将全部数据读取到内存中，减小电脑压力。

为了方便计算Sigmoid函数的值，添加如下方法：

#S型函数
def sigmoid(x):
    return 1./(1+np.exp(-x))

Logistic逻辑回归实现代码如下：

#拟合参数
def grad_ascent(dataset, labels, alpha=0.001, max_cycles=500):
    dataset = np.mat(dataset)
    labels = np.mat(labels).transpose()
    
    m, n = np.shape(dataset)
    weights = np.ones((n, 1)) #初始化参数
    trans_dataset = dataset.transpose()
    
    for k in range(max_cycles):
        #使用S型函数分类
        h = sigmoid(dataset*weights) 
        
        #梯度上升
        weights = weights + alpha*trans_dataset*(labels-h)
    return weights

梯度上升这里，利用到矩阵的乘法运算，通过numpy库将数据转成矩阵并快速计算。

我们可以加个测试执行代码：

if __name__ == '__main__':
    dataset, labels = load_dataset()
    weights = grad_ascent(dataset, labels)
    print(weights)

可以得到边界线的最后拟合结果。

若你安装了matplotlib图表库，可用如下代码画图直观展示效果：

#coding:utf-8
import matplotlib.pyplot as plt

#画图
def plot_graph(dataset, labels, weights):
    dataset = np.array(dataset)
    m, n = np.shape(dataset)
    
    #数据分组
    r_x1 = []
    r_x2 = []
    g_x1 = []
    g_x2 = []
    
    for i in range(m):
        if labels[i] == 1:
            r_x1.append(dataset[i, 1])
            r_x2.append(dataset[i, 2])
        else:
            g_x1.append(dataset[i, 1])
            g_x2.append(dataset[i, 2])

    #画数据点
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(r_x1, r_x2, s=30, c='red', marker='s')
    ax.scatter(g_x1, g_x2, s=30, c='green')
    
    #画边界线
    x1 = np.arange(-3., 3., 0.1)
    x2 = (-weights[0] - weights[1]*x1)/weights[2]
    ax.plot(x1, x2.transpose())

    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.show()

其中，画边界线的代码需要说明一下。

边界线的线性方程为 z = θ₀X₀+θ₁X₁+θ₂X₂ , 其中X₀=1。

又因为z=0是分类的边界。所以代入方程得：

0 = θ₀+θ₁X₁+θ₂X₂

最后，转化得到：

X₂ = (- θ₁X₁ -θ₀)/θ₂

绘图效果如下：

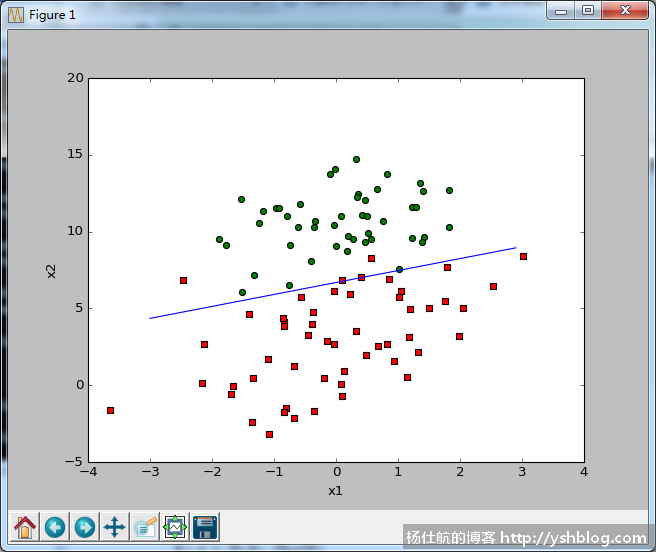
拟合效果还是比较不错。不过每次计算都要拿全部样本的数据计算。所以该方法也叫批梯度上升。

而且上升过程中和步长α以及迭代次数有关，可能拟合不足或过度拟合。大家可以调整相关参数测试一下。

后面会用随机梯度上升算法优化。

得到边界线的线性方程之后，有新的数据点可以求解得到对应的g(z)和0.5比较得到分类。这个比较简单就不演示。

点击查看相关目录。

参考文档：

斯坦福机器学习第六课笔记：http://blog.chinaunix.net/uid-20761674-id-4336428.html

最大似然估计：http://edu6.teacher.com.cn/ttg006a/chap7/jiangjie/72.htm

逻辑回归1：http://blog.csdn.net/star_liux/article/details/39666737

逻辑回归2：http://blog.csdn.net/huruzun/article/details/40076869

上一篇：机器学习10：逻辑回归优化

下一篇：我的网站搭建(第49天) 评论框使用emoji表情

相关专题： 机器学习实战