上篇博文详细讲解什么是逻辑回归(Logistic回归)：机器学习09：逻辑回归详解

文中每次拟合的时候，使用全部训练集的数据。计算量大，有可能训练集的样本有成千上百万。而且可能出现拟合不足或拟合过度，因为其中迭代次数是我们直接指定。不一定每次都可以找到合适的迭代次数。

所以，需要改进逻辑回归拟合的算法。

既然使用全部样本的数据来更新边界线的回归系数计算量很大。

那么，我们可以尝试每次迭代的时候，只使用一个样本。

基于上篇博文：机器学习09：逻辑回归详解的代码（包括获取训练集，S型函数，绘图方法等等）

#coding:utf-8
import numpy as np

#获取训练集
def load_dataset(filename='testSet.txt'):
    dataset = []
    labels = []
    with open(filename, 'r') as f:
        line = f.readline()
        while line != '':
            data = line.strip().split()
            dataset.append([1., float(data[0]), float(data[1])])
            labels.append(int(data[2]))
            line = f.readline()

    return dataset, labels

#S型函数
def sigmoid(x):
    return 1./(1+np.exp(-x))

绘图方法，需要安装Python的图表matplotlib库。

#coding:utf-8
import matplotlib.pyplot as plt

#画图
def plot_graph(dataset, labels, weights):
    dataset = np.array(dataset)
    m, n = np.shape(dataset)
    
    #数据分组
    r_x1 = []
    r_x2 = []
    g_x1 = []
    g_x2 = []
    
    for i in range(m):
        if labels[i] == 1:
            r_x1.append(dataset[i, 1])
            r_x2.append(dataset[i, 2])
        else:
            g_x1.append(dataset[i, 1])
            g_x2.append(dataset[i, 2])

    #画数据点
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(r_x1, r_x2, s=30, c='red', marker='s')
    ax.scatter(g_x1, g_x2, s=30, c='green')
    
    #画边界线
    x1 = np.arange(-3.5, 3.5, 0.1)
    x2 = (-weights[0] - weights[1]*x1)/weights[2]
    ax.plot(x1, x2.transpose())

    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.show()

相关代码就这些，具体逻辑回归分析可见上一篇博文：机器学习09：逻辑回归详解

接下来修改拟合方法的代码如下：

#每次计算使用一个样本
def stoc_grad_ascent(dataset, labels, alpha=0.01):
    dataset = np.array(dataset)
    m, n = np.shape(dataset)
    weights = np.ones(n)

    for i in xrange(m):
        h = sigmoid(sum(dataset[i] * weights))
        error = labels[i] - h
        weights = weights + alpha * error * dataset[i]
    return weights

该方法结果如下图所示：

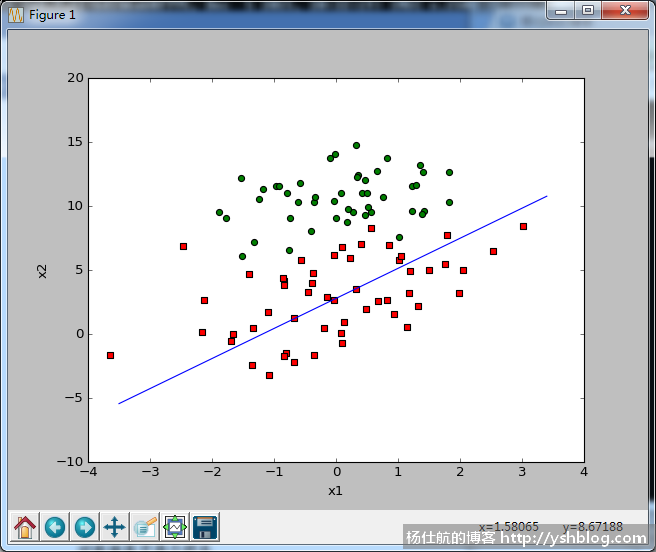
可以看出，这个边界线明显不是最佳的拟合结果，拟合不足。

原先的批量计算迭代了500次，步长为0.001；

修改之后的计算迭代了m次，这里有100个样本。即迭代了100次，步长为0.01。

既然拟合不足，那么我们可以多迭代几次。修改代码如下：

#每次计算使用一个样本，重复迭代全部样本150次
def stoc_grad_ascent(dataset, labels, alpha=0.01):
    dataset = np.array(dataset)
    m, n = np.shape(dataset)
    weights = np.ones(n)

    for j in range(150):
        for i in xrange(m):
            h = sigmoid(sum(dataset[i] * weights))
            error = labels[i] - h
            weights = weights + alpha * error * dataset[i]
    return weights

结果如下：

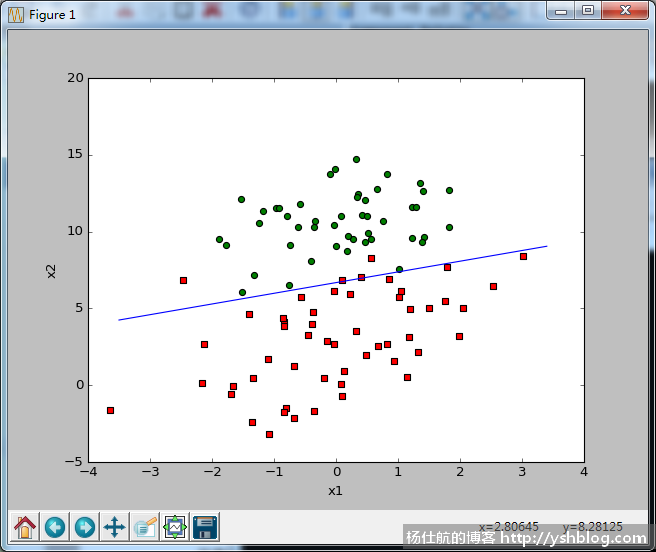
可看出，这次拟合效果比较好。

虽然迭代了150次全部样本。相当于计算了150*100=15000个样本计算。

相对批量计算500次的全部样本，相当与计算了500*100=50000个样本计算。

可见，使用一个样本的计算量小很多。

我们还可以继续优化拟合方法的代码。

首先从步长入手。这个步长是控制拟合速度。

若步长设置越大，拟合速度越快，迭代次数较少，但精确度不是较高的；

若步长设置越小，拟合速度越慢，拟合精确度越高，但需要更多次迭代计算。

通俗点说，每次迈出的脚步距离一样长。步子跨大了，跑得比较快，但可能越过终点。步子迈小了，到达终点的耗时较长。

所以，我们可以考虑一开始步长大一些，越靠近终点，步长越小，令其拟合更好。

修改代码如下：

#coding:utf-8
import random

#随机梯度上升
def stoc_grad_ascent2(dataset, labels, num_iter=150):
    dataset = np.array(dataset)
    m, n = np.shape(dataset)
    weights = np.ones(n)

    for j in range(num_iter):
        for i in range(m):
            alpha = 4/(1. + j + i*0.1) + 0.001 #步长调整
            rand_index = int(random.uniform(0, m - i)) #随机获取样本

            h = sigmoid(sum(dataset[rand_index] * weights))
            error = labels[rand_index] - h
            weights = weights + alpha * error * dataset[rand_index]
    return weights

此处，还加了随机获取样本的处理。该处理是为了消除一些不确定因素造成的数据波动。

该方法称为随机梯度上升，绘图结果如下：

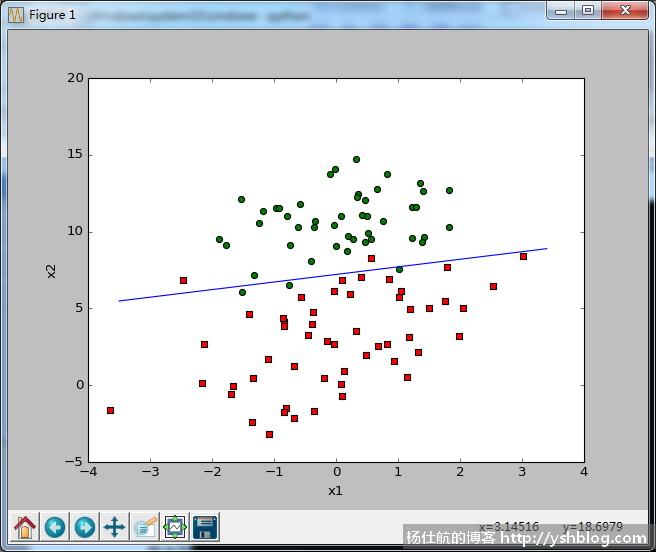
当然，你也可以调整迭代次数，令其拟合效果更好。

点击查看相关目录。

上一篇：VSTO插件无法运行和解决方法

下一篇：机器学习09：逻辑回归详解

相关专题： 机器学习实战