之前简单用Numpy的二维矩阵结构解过数独：Python秒解最难数独

闲暇之余，产生另外一个想法：用Python生成数独题目。

1、初次尝试

经典数独是9*9的方阵。最简单的生成题目思路是按照从左至右，从上至下的顺序逐个把1~9的数字随机填入到数独的格子中。然后再随机抹去一定数量的格子即可。

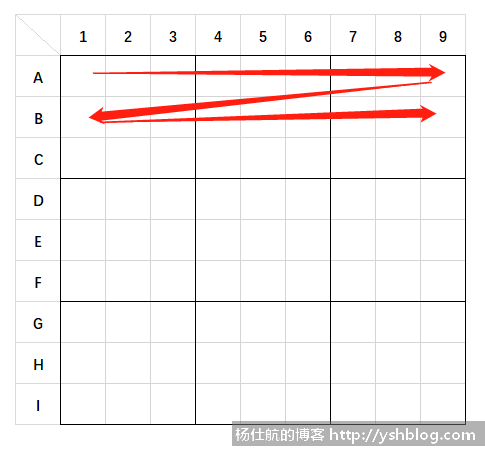
当然，这里随机填入的时候，还要考虑到数独的规则：

1）同一行的数字不能重复

2）同一列的数字不能重复

3）同一个九宫格的数字不能重复

所以，在随机填入的时候，每次填入之前都要检查是否符合上面的条件。或者在随机生成数字的时候，就把所在格子的行、列、九宫格已经存在的数字排除在外，然后再生成随机数字。

我采取排除的方法生成随机数字，简单代码如下：

1）先定义获取一个二维矩阵行、列、九宫格的方法

import random
import numpy as np


# 其中sudo参数是numpy的二维矩阵
# 获取格子所在的行的全部格子
def get_row(sudo, row):
    return sudo[row, :]

# 获取格子所在的列的全部格子
def get_col(sudo, col):
    return sudo[:, col]

# 获取格子所在的九宫格的全部格子
def get_block(sudo, row, col):
    row_start = row // 3 * 3
    col_start = col // 3 * 3
    return sudo[row_start: row_start + 3, col_start: col_start + 3]

2）书写生成逻辑：遍历，排除已被使用的数字，随机填入

def create():
    # 1~9，参考一维数组
    sample = np.array(range(1, 10))
    # 9*9的二维矩阵，每个格子默认值为0
    sudo = np.zeros((9, 9), dtype=int)

    # 遍历从左到右，从上到下逐个遍历
    for row in range(9):
        for col in range(9):
            # 获取该格子对应的行、列、九宫格
            sudo_row = get_row(sudo, row)
            sudo_col = get_col(sudo, col)
            sudo_block = get_block(sudo, row, col)

            # 该格子已被使用的数字，并集运算
            used_nums = np.union1d(np.union1d(sudo_row, sudo_col), sudo_block)
            # 剩下可用的数字,差集运算
            rest_nums = np.setdiff1d(sample, used_nums)

            # 判断是否有数字可用
            if len(rest_nums) == 0:
                raise Exception('发生错误，没有数字可用')
            
            # 随机取出一个
            rand_num = random.sample(rest_nums.tolist(),1)[0]
            sudo[row, col] = rand_num
    return sudo

3）执行

我尝试执行，都遇到没有数字可用的错误

调整代码，打印发生错误时的数独

# 打印数独
def print_sudo(sudo):
    for row_index, row in enumerate(sudo):
        if row_index % 3 == 0 and row_index != 0:
            print('-' * (9 + 8 + 4))
        row = list(map(str, row.tolist()))
        row.insert(6, '|')
        row.insert(3, '|')
        print(' '.join(row))

def create():
    # 1~9，参考一维数组
    sample = np.array(range(1, 10))
    # 9*9的二维矩阵，每个格子默认值为0
    sudo = np.zeros((9, 9), dtype=int)

    # 遍历从左到右，从上到下逐个遍历
    for row in range(9):
        for col in range(9):
            # 获取该格子对应的行、列、九宫格
            sudo_row = get_row(sudo, row)
            sudo_col = get_col(sudo, col)
            sudo_block = get_block(sudo, row, col)

            # 该格子已被使用的数字，并集运算
            used_nums = np.union1d(np.union1d(sudo_row, sudo_col), sudo_block)
            # 剩下可用的数字,差集运算
            rest_nums = np.setdiff1d(sample, used_nums)

            # 判断是否有数字可用
            if len(rest_nums) == 0:
                print_sudo(sudo)
                raise Exception('发生错误，[{0}, {1}]没有数字可用'.format(row + 1, col + 1))
            
            # 随机取出一个
            rand_num = random.sample(rest_nums.tolist(),1)[0]
            sudo[row, col] = rand_num
    return sudo

再次执行：

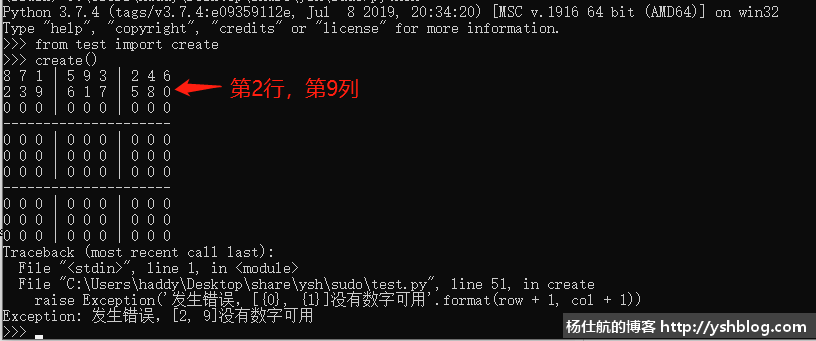
执行结果，第2行第9列没有数字可用。

我们看第2行已经几乎填满了数字，剩下4可填。而在这个九宫格，数字4已经被使用（第1行第8列）。所以无数字可用。

4）初步结论

后来，我又尝试了好几次，都是出现这种结果。仔细思考，得出以下结论：

以上面的例子为例，第二行在随机填写数字的时候，没有考虑到数字4在后面3列无法使用。除了数独基本3个限制条件外，其实这3个限制条件会导致数字之间产生一种纠缠关系。而前面简单的做法没有考虑到这种潜在的影响，所以无法生成一个完整的数独。

从数独的3个限制条件出发，3个限制条件都是不同的维度。而这些维度都有交叉关系，例如一个格子同时存在于某一行和某一列、某一九宫格。就像空间坐标轴，空间上的任意一点都有x、y、z等3个坐标轴。

感觉数独是一种高纬度的矩阵，我们看到的二维矩阵只是高纬度矩阵在二维上的投影。如果用这种简单随机方法生成数独的话，很难涉及到每个数字之间的纠缠关系，可能需要用更高维度的方式去处理，例如3维矩阵、4维矩阵。

后来，我尝试提高维度去解决问题，也遇到同样无法直接生成数独。可能我的数学知识还不够，不能用数学的方式表达数独。

其实用我之前解数独的方法也可以生成数独。在生成的过程发现有问题就回退上一步，重新选择其他随机数。相当于解一个81个格子都为空的数独。用这个方法没多大意思，一来是我已经做过的了，二来效率其实不太高。

2、柳暗花明又一村

在不断翻阅资料时，偶然发现一个规律：在已有的数独结果上，同一个九宫格内任意两个格子，调换其所在的行或者所在的列后的结果，还是一个有效的数独。

例如交换D1和E3两个格子所在的行：

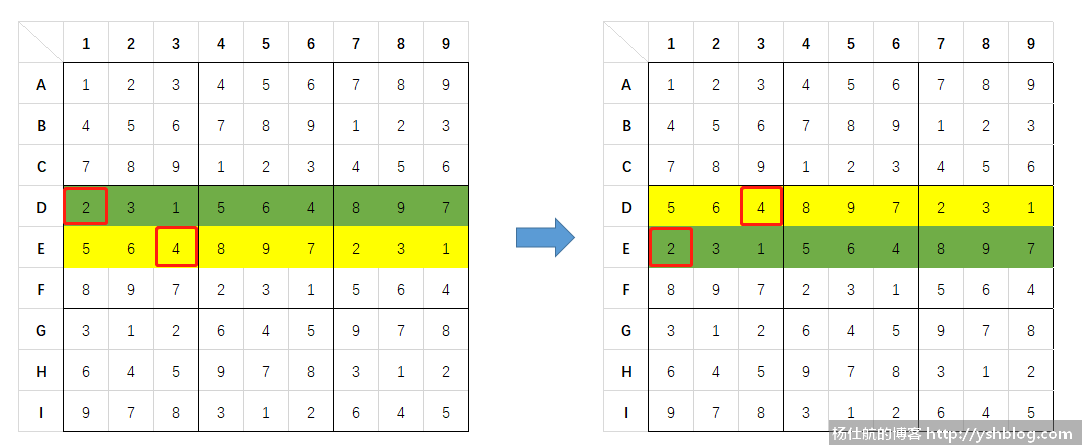
数独3个限制条件都没有被破坏。进一步发现，其实只要在九宫格范围里面的任意两行或两列交换都可以。

例如交换D行和E行，D行和E行都在九宫格的范围内。而A行和D行就不能交换。

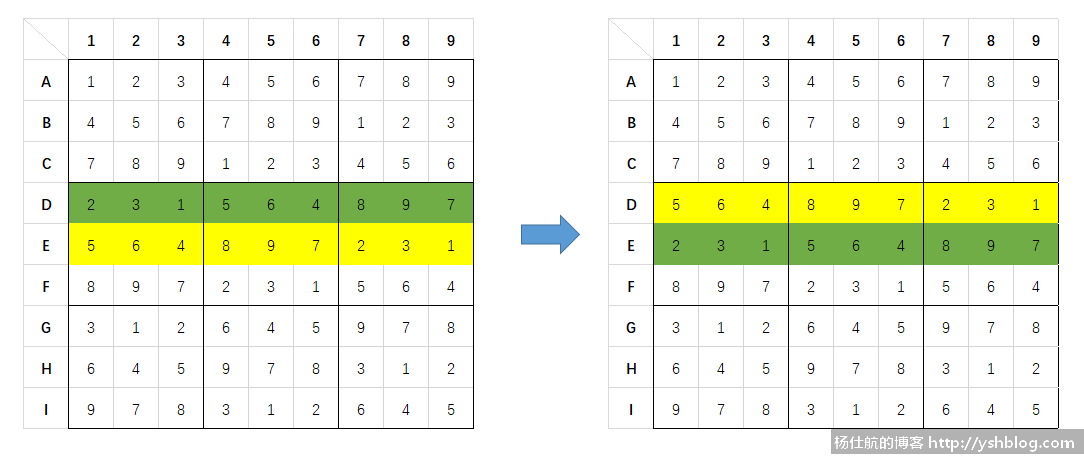
如此一来，我们只要用一个简单的数独（这个术语叫基本盘），随机多次交换不会破坏数独完整性的行或列，形成最终结果（术语叫终盘）；最后再随机抹去一些数据即可变成数独题目。

1）生成基本盘

生成基本盘的代码如下（延用上面的get_row、get_col、get_block方法）：

def create_base_sudo():
    # 9*9的二维矩阵，每个格子默认值为0
    sudo = np.zeros((9, 9), dtype=int)
    # 随机生成起始的基数(1 ~ 9)
    num = random.randrange(9) + 1

    # 遍历从左到右，从上到下逐个遍历
    for row_index in range(9):
        for col_index in range(9):
            # 获取该格子对应的行、列、九宫格
            sudo_row = get_row(sudo, row_index)
            sudo_col = get_col(sudo, col_index)
            sudo_block = get_block(sudo, row_index, col_index)

            # 如果该数字已经存在于对应的行、列、九宫格
            # 则继续判断下一个候选数字，直到没有重复
            while num in sudo_row or num in sudo_col or num in sudo_block:
                num = num % 9 + 1

            # 赋值
            sudo[row_index, col_index] = num
            num = num % 9 + 1
    return sudo

这里用了求余的方法，把num限制在1到9之间。执行该方法，可以得到如下类似的基本盘：

2）随机交换，得到终盘

然后我们再多次随机交换行列，得到终盘：

# 随机交换n次
def random_sudo(sudo, times):
    for _ in range(times):
        # 随机交换两行
        rand_row_base = random.randrange(3) * 3  # 从0，3，6 随机取一个
        rand_rows = random.sample(range(3), 2)   # 从 0，1，2中随机取两个数
        row_1 = rand_row_base + rand_rows[0]
        row_2 = rand_row_base + rand_rows[1]
        sudo[[row_1, row_2], :] = sudo[[row_2, row_1], :]

        # 随机交换两列
        rand_col_base = random.randrange(3) * 3
        rand_cols = random.sample(range(3), 2)
        col_1 = rand_col_base + rand_cols[0]
        col_2 = rand_col_base + rand_cols[1]
        sudo[:, [col_1, col_2]] = sudo[:, [col_2, col_1]]

我随机交换50次，最终得到一个和基本盘差别很大的终盘：

3）随机抹去数字，得到数独题目

这里如果抹去数字太多，会导致题目很难解，或者容易有多个解；如果抹去数字太少，数独题目就会变得很简单。

经过一番测试，大概最多清除64个数字，最少清除14个数字，得到的题目可解。代码如下：

def get_sudo_subject(sudo, del_nums):
    # 最少要保留17个数字，题目才可解。一共81个数字，则最多可以擦除81-17 = 64。
    max_clear_count = 64
    # 最少也要擦除14个
    min_clear_count = 14

    if del_nums < min_clear_count:
        del_nums = min_clear_count
    if del_nums > max_clear_count:
        del_nums = max_clear_count

    # 随机擦除（从0到80，随机取要删除的个数）
    clears = random.sample(range(81), del_nums)
    for clear_index in clears:
        # 把0到80的坐标转化成行和列索引
        # 这样就不会重复删除同一个格子的数字
        row_index = clear_index // 9
        col_index = clear_index % 9
        sudo[row_index, col_index] = 0

下面是我随机抹去30个数字的效果：

4）整合代码

这里除了整合全部代码之外，我还划分了难度等级，抹去数字越多则越难。我将其划分为5个级别：入门、初级、熟练、精通、大神。

具体代码如下：

import random
import numpy as np


# 获取格子所在的行的全部格子
def get_row(sudo, row):
    return sudo[row, :]

# 获取格子所在的列的全部格子
def get_col(sudo, col):
    return sudo[:, col]

# 获取格子所在的九宫格的全部格子
def get_block(sudo, row, col):
    row_start = row // 3 * 3
    col_start = col // 3 * 3
    return sudo[row_start: row_start + 3, col_start: col_start + 3]

# 打印数独
def print_sudo(sudo):
    for row_index, row in enumerate(sudo):
        if row_index % 3 == 0 and row_index != 0:
            print('-' * (9 + 8 + 4))
        row = list(map(str, row.tolist()))
        row.insert(6, '|')
        row.insert(3, '|')
        row_str = ' '.join(row)
        print(row_str.replace('0', ' '))

def create_base_sudo():
    # 9*9的二维矩阵，每个格子默认值为0
    sudo = np.zeros((9, 9), dtype=int)
    # 随机生成起始的基数(1 ~ 9)
    num = random.randrange(9) + 1

    # 遍历从左到右，从上到下逐个遍历
    for row_index in range(9):
        for col_index in range(9):
            # 获取该格子对应的行、列、九宫格
            sudo_row = get_row(sudo, row_index)
            sudo_col = get_col(sudo, col_index)
            sudo_block = get_block(sudo, row_index, col_index)

            # 如果该数字已经存在于对应的行、列、九宫格
            # 则继续判断下一个候选数字，直到没有重复
            while num in sudo_row or num in sudo_col or num in sudo_block:
                num = num % 9 + 1

            # 赋值
            sudo[row_index, col_index] = num
            num = num % 9 + 1
    return sudo

def random_sudo(sudo, times):
    for _ in range(times):
        # 随机交换两行
        rand_row_base = random.randrange(3) * 3  # 从0，3，6 随机取一个
        rand_rows = random.sample(range(3), 2)   # 从 0，1，2中随机取两个数
        row_1 = rand_row_base + rand_rows[0]
        row_2 = rand_row_base + rand_rows[1]
        sudo[[row_1, row_2], :] = sudo[[row_2, row_1], :]

        # 随机交换两列
        rand_col_base = random.randrange(3) * 3
        rand_cols = random.sample(range(3), 2)
        col_1 = rand_col_base + rand_cols[0]
        col_2 = rand_col_base + rand_cols[1]
        sudo[:, [col_1, col_2]] = sudo[:, [col_2, col_1]]

def get_sudo_subject(sudo, del_nums):
    subject = sudo.copy()

    # 随机擦除（从0到80，随机取要删除的个数）
    clears = random.sample(range(81), del_nums)
    for clear_index in clears:
        # 把0到80的坐标转化成行和列索引
        # 这样就不会重复删除同一个格子的数字
        row_index = clear_index // 9
        col_index = clear_index % 9
        subject[row_index, col_index] = 0
    return subject

if __name__ == '__main__':
    max_clear_count = 64  # 最多清除个数
    min_clear_count = 14  # 最少清除个数

    # 设置难度等级，1~5，5个等级：入门、初级、熟练、精通、大神
    level = 3
    
    # 每个等级的个数
    each_level_count = (max_clear_count - min_clear_count) / 5

    # 该等级最小数
    level_start = min_clear_count + (level - 1) * each_level_count
    # 该等级范围内的随机数
    del_nums = random.randrange(level_start, level_start + each_level_count)

    # 生成基本盘
    sudo = create_base_sudo()
    # 生成终盘
    random_sudo(sudo, 50)
    # 获取数独题目
    subject = get_sudo_subject(sudo, del_nums)

    print('题目：')
    print('=' * 26)
    print_sudo(subject)
    print('\n答案：')
    print('=' * 26)
    print_sudo(sudo)

生成熟练等级的数独题目，执行结果如下：

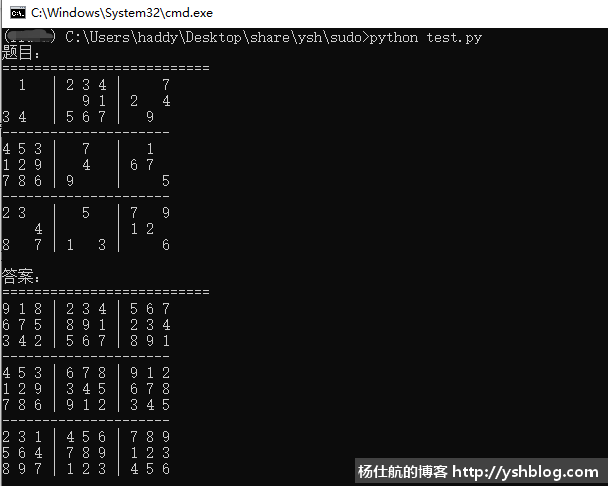
上一篇：没有了

下一篇：MySQL忘记root密码【来自官方文档的方法，亲测有用】

相关专题： 我为数独迷