位运算是直接对整数在二进制中进行操作。另我们的电脑电路设计都是基于二进制的，所以在二进制层面效率很高。通常位运算多用在对程序效率要求很高的场景。

在说位运算符之前，先科普一下二进制相关的术语，以及如何转换。

以下的二进制都以8位为例。第1位是符号位，后面7位是数字位。符号位用0代表非负数，用1代表负数。

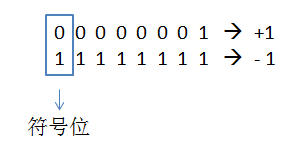
术语1：原码

原码是二进制的一种表现方式。取该整数的绝对值的二进制，再加上符号位。例如

该原码只是为了让我们看二进制更直观，直接看出正负数和比较大小。但原码不是计算机保存的二进制，所以不能直接参与计算。

术语2：反码

反码主要是针对负数的处理。在原码的基础上，符号位不变，其他数值位取反，即把1变成0，把0变成1。

反码是为了在计算机中存储二进制，但非真正的二进制值，所以也不直接参与计算。

术语3：补码

补码是真正的二进制值了，主要也是针对负数。非负数不变，而负数是在反码的基础上加1。

说了这么多，最终需要记住有两点：

1、正数的二进制值，原码、补码、反码都是一样的；

2、负数的二进制值是其补码，即反码加1。

科普完二进制的知识，继续讲位运算。在Python中，位运算符常用有6种：

1）按位与（&）

2）按位或（|）

3）按位异或（^）

4）按位翻转（~）

5）左移运算（<<）

6）右移运算（>>）

1、按位与（&）

按位与，即按照对应位置的二进制and比较。可以把1当作true，把0当作false。1 and 1 = 1，1 and 0 = 0，0 and 1 = 0，0 and 0 = 0，如下示意图：

5&3结果为1。

那这个有什么用呢？

举个例子：判断数字是奇数还是偶数。普通判断方法求数字除以2求余。

n%3 == 1  #True为偶数，False为奇数

可以用按位与运算判断奇偶，运算效率要高很多。

n&1 == 1  #按位于运算奇数返回1，偶数返回0

2、按位或（|）

按位或，即安装对应位置的二进制or比较。1 or 1 = 1，1 or 0 = 1，0 or 1 = 1，0 or 0 = 0。例如：

5|3结果为7。

我们可以利用这个方法对数值修正，例如取每个整数向上去奇数。

map(lambda x:x|1, range(6))

结果返回 [1, 1, 3, 3, 5, 5]。若在这个基础上减1，可以得到向下取偶数。

3、按位异或（^）

按位异或，则是按照对应位置的二进制xor比较。1 xor 1 = 0，1 xor 0 = 1，0 xor 1 = 1，0 xor 0 = 0。例如：

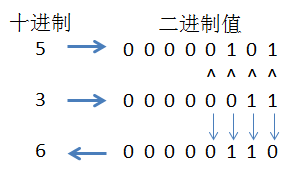
5^3结果为6。

出一道算法题目：已知一个数字数组。其中只有一个数字只出现1次，其他数字都出现2次。求只出现1次的数字。

例如，[1,1,3,2,4,3,4]，只出现1次的数字是2。

普通做法可以用字典处理：

def get_one(nums):
    nums_dict = {}
    for num in nums:
        #遍历数字列表，并累计统计
        nums_dict[num] = nums_dict.get(num, 0) + 1
    for key, value in nums_dict.iteritems():
        if value==1:
            #返回值为1的键值
            return key

但这样效率比较慢，遍历了两次。可以利用按位异或1个特性：自己和自己异或为0，优化算法。把全部值按位异或计算，出现两次的值就抵消，最后保留下来的是只出现一次的数字。

def get_one(nums):
    return reduce(lambda x,y: x^y, nums)

利用reduce函数，一句话代码搞定且效率很高。

4、按位翻转（~）

按位翻转，即不管符号位还是数值位，全部取反码。即1变成0，0变成1。

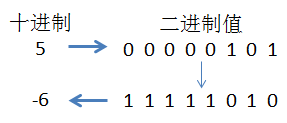
这个翻转比较容易理解，就不多说。

另外翻转和按位异或有关系，翻转相当于和-1按位异或：~n = n^-1。

5、左移运算（<<）

左移运算是将二进制数值整体向左边移动n个位置，空出来的位置补0。例如5<<2：

左移两位，数字5变成20，多了4倍。而从二进制看多了100倍。十进制的4等于二进制的100。这么看来左移运算可以用于乘法计算。

再举个例子十进制5*7 = 101B * 111B。111B这个不是10的指数(10的n次方)，那么需要对111B拆分成100B+10B+1B。即：

  5 * 7
= 101B * 111B
= 101B * (100B + 10B + 1B)
= 101B * 100B + 101B * 10B + 101B * 1B
= 5<<2 + 5<<1 + 5<<0
= 20 + 10 + 5
= 35

虽然看起来繁琐一些，但实际运算效率要比简单相乘快很多。

6、右移运算（>>）

右移运算是将二进制数值整体向右边移动n个位置，空出来的位置补上符号位的数值。即正数补0，负数补1。

这个右移运算可以类似上面左移运算用于乘法一样，用于除法。这个你可以自己尝试一下。

右移了两位相当于101B除以100B，二进制100B对应十进制是3。

可以发现该除法计算是取结果的整数部分，5/3 = 1。这个和Python2.7的除法运算结果一样。

大致Python按位运算讲这些内容。出一道题：判断一个数是否是2的指数。

ps：本道题虽然可以用math模版的log求解，但效率不是更高。可以试试按位与运算。

上一篇：我的网站搭建(第35天) 用UEditor新增博文

下一篇：UEditor使用prettify.js处理代码高亮