上次讲了最快的排序算法之一：快速排序算法。而快速排序不是一个稳定的算法，在交换过程中可能进入胡同一直在几个数字之间处理。这次将仔细讲解归并排序算法，一个稳定快速的排序算法。

归并排序采用分组处理，也是二分法的思想。将一组数据拆成两组，再将小组继续拆分为两个直到每个小组剩下1或0个元素。这时才开始对小组中的元素排序，排序完成之后再合并为新的小组。一直往上排序和合并直到排序完成。文字还是看不懂？或者我描述不清楚？看图，先是拆分，很明显的二分法思想：

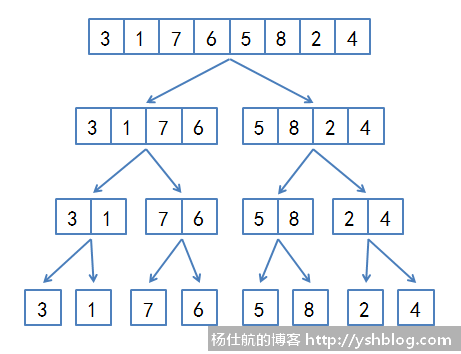
再拿最底层的数据开始合并和排序，如图一层层比较：

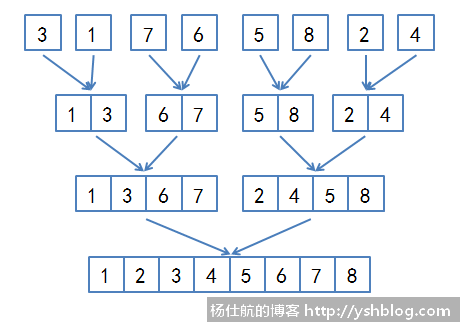
这里需要思考两个东西：

1）如何拆分

2）如何合并且排序

先写拆分代码，根据列表长度使用切片器将其拆分成两半：

def split(lists):
    mid = len(lists) / 2
    left = lists[:mid]
    right = lists[mid:]

拆成两部分之后，还有继续拆分，直到剩下1或0个元素。这里可以采用递归：

def split(lists):
    # 递归退出条件判断
    length = len(lists)
    if length <= 1:
        return lists
        
    # 取整，兼容py3
    mid = length // 2
    left = lists[:mid]
    right = lists[mid:]
    
    # 递归拆分
    split(left)
    split(right)

这段代码不完善，除了列表长度小于等于1的时候，才返回结果。其他情况未返回结果，也就是说拆分之后就没有后续处理。这个地方留给排序代码，将拆分后的列表合并和排序。

那么合并排序的方法需要两个参数，两个list列表。由于我们每次排序都是基于上次合并排序后的结果。所以可以按照顺序抽取两个list的元素判断大小，并添加到新的列表中，完成合并排序的步骤。代码如下：

def merge(left, right):
    i = 0
    j = 0
    result = []
    length_left = len(left)
    length_right = len(right)
    
    while i < length_left and j < length_right:
        # 逐个比较两个列表的元素
        # 小的添加进新列表，大的留下继续比较
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
            
    # 最后加上未比较的元素
    result.extend(left[i:])
    result.extend(right[j:])
    return result

再修改拆分的代码，加入合并排序的代码：

def split(lists):
    # 递归退出条件判断
    length = len(lists)
    if length <= 1:
        return lists
        
    # 递归拆分，取整，兼容py3
    mid = length // 2
    left = split(lists[:mid])
    right = split(lists[mid:])
    
    # 合并排序（归并排序）
    return merge(left, right)

可能有些人看不懂代码了，就加了一句合并排序的代码，就完成归并排序。

递归需要从最后面的步骤逆推，倒着想。当只有1个元素时返回lists拆分的结果，再两个1个元素的left和right列表合并排序。排序完成之后再返回一次合并排序后的列表。该返回结果是2个元素拆分之后的结果，再继续合并排序，继续返回结果给上一层。直到排序结束。完整代码如下，为了一目了然看出这是归并排序，修改方法名：

#coding:utf-8
def merge(left, right):
    '''合并和排序'''
    i = 0
    j = 0
    result = []
    length_left = len(left)
    length_right = len(right)
    
    while i < length_left and j < length_right:
        # 逐个比较两个列表的元素
        # 小的添加进新列表，大的留下继续比较
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
            
    # 最后加上未比较的元素
    result.extend(left[i:])
    result.extend(right[j:])
    return result
    
def merge_sort(lists):
    '''归并排序入口，拆分列表'''
    # 递归退出条件判断
    length = len(lists)
    if length <= 1:
        return lists
        
    # 递归拆分，取整，兼容py3
    mid = length // 2
    left = merge_sort(lists[:mid])
    right = merge_sort(lists[mid:])
    
    # 合并排序（归并排序）
    return merge(left, right)

可用如下代码测试：

import random

lists = random.sample(range(2000000), 1000000)
result = merge_sort(lists)

使用random模块生成1百万个随机数进行归并排序。

在我的电脑测试大概耗时5、6秒，相对快速排序算法是慢了一点（快速排序耗时大概1、2秒），但它稳定。

上一篇：Django使用第三方存储服务器

下一篇：Python实现快速排序算法