可能有些人问排序算法有什么用？好像除了考试和找工作面试之外，很少需要用得到。

其实不然，以前硬件配置较低，排序花费时间很长，需要通过算法进行一系列的优化。现在硬件配置高了，但处理大量的数据时也需要使用排序算法，提高执行效率。例如信息检索、科学计算等等。

排序算法有不少，可自行搜索看看有哪些。这里详细讲讲快速排序的思路和实现方法。

快速排序是目前已知排序算法中最快的算法之一。有2百万个元素的List在短短几秒内完成排序。如果这个List你用Python自带的sort方法，分分钟别人和你的友谊翻船。

它的基本思路也不难：在一个数据集中取个数作为参考点，大于该数的元素放在其右边；小于该数的元素放在其左边。这样就将数据集分成两部分，大于参考值部分和小于参考值部分。如下图所示：

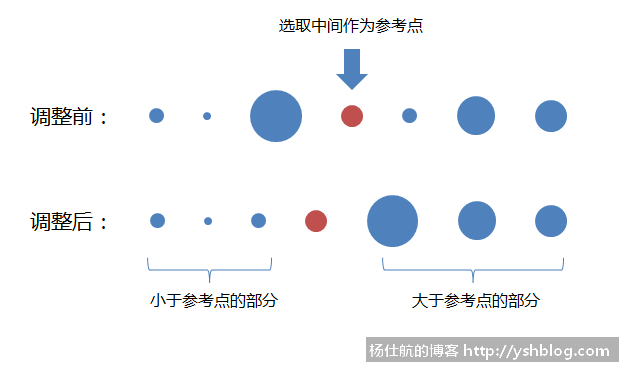
鉴于数据过于枯燥，用圆形的面积代表大小。

划分两大部分之后，再继续对这两部分重复上面的方法。分别对那两部分继续排序调整，一直重复下去知道排序完成。如下图所示：

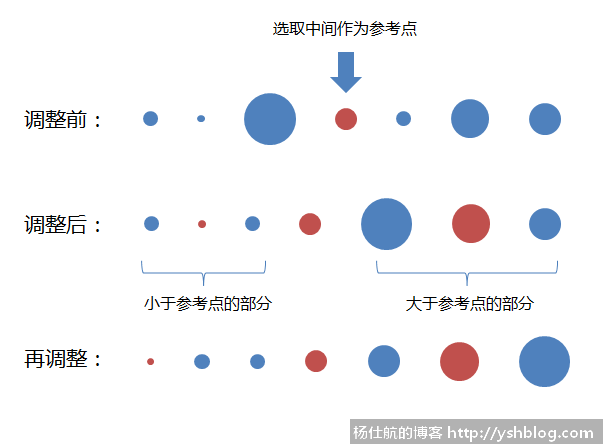
通过第2次调整就完成排序了。你有没有发现快速排序中有二分法的思想。根据参考点分成两部分再对细分的部分重复循环处理直到完成排序。

那么，Python如何实现快速排序？

重复循环处理的步骤可以用循环或递归实现。重点是如何确定参考点以及如何把小于参考点的值挪到左边；把大于参考点的值挪到右边。为了方便计算，参考点可以选中第1个元素再进行判断和交换值。如下代码：

#coding:utf-8
def quick_sort(lists):
    '''快速排序的一次调整'''
    # 获取调整的范围
    left = 0
    right = len(lists) - 1    
    key = lists[left]   # 选择参考点，该调整范围的第1个值

    # 从右边开始查找大于参考点的值
    while lists[right] >= key:
        right -= 1
    lists[left] = lists[right]  # 这个位置的值先挪到左边

    # 从左边开始查找小于参考点的值
    while lists[left] <= key:
        left += 1
    lists[right] = lists[left]  # 这个位置的值挪到右边

    # 写回改成的值
    lists[left] = key

代码看不懂？那就看图吧：

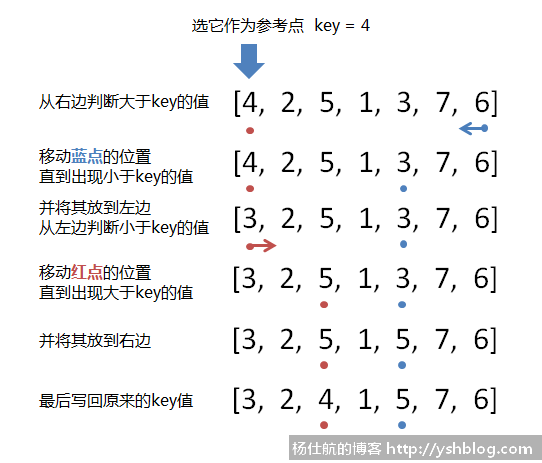
这里还有几个问题，从上图得出有可能中间有些值未判断到。那么调整之后还需要继续判断。另外left左边的点判断位置可能越过right右边的点，所以需要加条件限制。修改代码如下：

#coding:utf-8
def quick_sort(lists):
    '''快速排序的一次调整'''
    # 获取调整的范围
    left = 0
    right = len(lists) - 1    
    key = lists[left]   # 选择参考点，该调整范围的第1个值

    # 循环判断直到遍历全部
    while left < right:
        # 从右边开始查找大于参考点的值
        while left < right and lists[right] >= key:
            right -= 1
        lists[left] = lists[right]  # 这个位置的值先挪到左边

        # 从左边开始查找小于参考点的值
        while left < right and lists[left] <= key:
            left += 1
        lists[right] = lists[left]  # 这个位置的值挪到右边

    # 写回改成的值
    lists[left] = key

left和right两个变量值一直变化，直到两个相遇则说明遍历完全部数据点。而且写会key值不需要每次都写回，只需要最后填入即可。接下来再修改这个方法，修改为可递归的，继续递归调整好的两个区域。如下代码：

#coding:utf-8
def quick_sort(lists, left, right):
    '''快速排序'''
    # 跳出递归判断
    if left >= right:
        return lists

    # 选择参考点，该调整范围的第1个值
    key = lists[left]
    low = left  
    high = right

    # 循环判断直到遍历全部
    while left < right:
        # 从右边开始查找大于参考点的值
        while left < right and lists[right] >= key:
            right -= 1
        lists[left] = lists[right]  # 这个位置的值先挪到左边

        # 从左边开始查找小于参考点的值
        while left < right and lists[left] <= key:
            left += 1
        lists[right] = lists[left]  # 这个位置的值挪到右边

    # 写回改成的值
    lists[left] = key

    # 递归，并返回结果
    quick_sort(lists, low, left - 1)    # 递归左边部分
    quick_sort(lists, left + 1, high)   # 递归右边部分
    return lists

由于需要指定范围处理，所以添加两个参数left和right。可是这个left和right的值可能会变化，为了后面和指定递归处理的范围，所以添加两个临时变量low和high记录初始位置。递归相当与循环，需要结束循环的条件。若left>=right时，则无需继续处理并返回结果即可。

可以用如下代码测试：

import random
lists = random.simple(range(2000000), 1000000)  # 随机生成1百万个数据
sort_lists = quick_sort(lists[:], 0, len(lists)-1)  #快速排序

为了比较排序前后结果，lists[:]可以创建一个一样的新列表对象。可以测试一下，几秒内完成排序算法。快速排序的速度是杠杠的。但快速排序不是稳定的算法，有时可能无法完成排序。若稳定性要求高的可以使用其他排序算法，例如归并排序。也是我下次将要写的博客内容。

上一篇：Python实现归并排序算法

下一篇：Python使用__new__方法实现单例模式