上一篇博文讲了朴素贝叶斯的理论知识。有了理论基础，就可以实践应用了。

机器学习有个重要的应用是对文档自动分类。

例如电子邮件、新闻报道、用户留言、博客文章等等各种文档。

每一种文档类型都会出现各种的专有名词或常用名词等等。我们人眼判断归类一般也是根据这些特征判断归类。

但有些时候分类的界限很模糊，可能可以被分成多种类型。而且有些词语在不同语境下有多种含义。

例如“狗”正常意思是指动物本身，但有时也被用于骂人的常用名词。

模糊的东西可以使用概率的方法应对。

下面我们将使用朴素贝叶斯的方法对文本进行分类：侮辱性和非侮辱性文本。

1、构建词汇表

对文本进行判断，我们需要先建立一个词汇表。

当然，我们不需要待分类的文档中全部所有被使用到的词汇。例如全部词汇有1000个词，朴素贝叶斯只需要用到其中10~20个特征就足够做出很好的判断。

另外，若只是一个单词或词语一般无法形成具体语境和含义。我们要以句子为单位作为依据。

那么，我们如何从一堆文本中取出我们需要的句子？

这一点在《机器学习实战》书中没有说明，而且直接给出几个句子作为示例（见书中第58页）。

这个后面有需要再讨论，一般可以根据词频来决定挑选哪些句子作为训练集。

新建一个bayes.py文件。写入创建训练集的代码：

#coding:utf-8
import numpy as np

def create_dataset():
    posting_list = [
        'my dog has flea problems help please',
        'maybe not take him to dog park stupid',
        'my dalmation is so cute I love him',
        'stop posting stupid worthless garbage',
        'mr licks ate my steak how to stop him',
        'quit huying worthless dog food stupid'
    ]
    posting_list = map(lambda x:x.split(' '), posting_list)

    #上面句子对应的性质，0代表非侮辱性句子，1代表侮辱性句子
    class_vect = [0, 1, 0, 1, 0, 1]
    return posting_list, class_vect

这里为了方便输入，我先输入整句话再用空格分割。（中文句子可以使用NLTK对中文分词，有兴趣可以自行网上搜索）

接着，使用训练集构造一个词汇表。该词汇表是训练集出现过的单词。

#根据训练集生成词汇表
def create_vocab_list(posting_list):
    '''对所有句子取并集，获取词汇表'''
    return list(reduce(lambda x,y:x|set(y), [set([])] + posting_list))

2、句子数字化（向量化）

生成词汇表是为了将句子数字化。句子都是字符串，不能直接用于计算。

计算只能使用数字。下面再添加将句子数字化的方法。

同样可以只用一句话搞定，不用向书中写得那么繁琐。

def set_of_words_to_vect(vocab_list, input_set):
    '''对比句子向量和词汇表，找到对应出现在词汇表的位置'''
    return map(lambda x: 1 if x in input_set else 0, vocab_list)

该句子数字化的方法是朴素贝叶斯分类器实现方式之一，叫贝努利模型。太拗口了，也叫词集模式。

该方式只考虑词是否出现，没考虑出现次数。即每个词的权重是一致的。

若需要考虑权重，需要使用另外一种实现方法：多项式模型，也叫词袋模式。（下篇文章介绍）

为了理解句子数字化，可以随便写个句子测试效果：

if __name__ == '__main__':
    #创建训练集
    posting_list, class_vect = create_dataset()

    #获取词汇表
    vocab_list = create_vocab_list(posting_list)

    #输出词汇表
    print(u'词汇表：')
    print(vocab_list)
    print('\n')

    #测试句子数字化结果
    posting = 'I love cute dog'.split(' ')
    print(posting)
    posting_vect = set_of_words_to_vect(vocab_list, posting)
    print(posting_vect)

测试结果如下图，该测试句子中各个单词出现的位置可以通过结果得知。

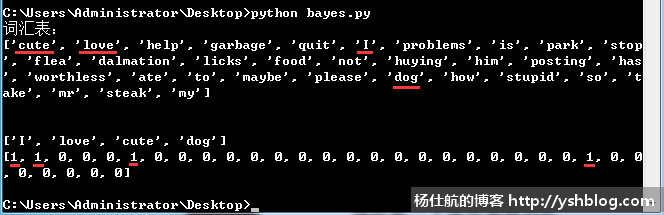
句子数字化也是句子向量化。该结果简称为词向量。

这里可以思考一下，若我输入一个句子，其中的单词在词汇表都不存在。句子数字化的结果将会是怎样的。

3、从词向量计算条件概率

通过前面两步，将文字的训练集向量化可以获得一个纯数字的训练集。该训练集都是词向量。

接下来，将利用训练集计算概率。

假设，我们句子转换后的词向量为w；c₁为侮辱性类别；c₀为非侮辱性类别。

根据上一篇博文的朴素贝叶斯的理论知识。我们需要比较词向量分别在这两个类别的条件概率：p(c₁|w) 和 p(c₀|w)。

哪个条件概率大就把词向量w归为哪种类别。（此处对应书中第60页，相信我，书中写得太难理解）

根据贝叶斯准则，转换一下该条件概率计算方法。

计算p(c₁|w) 和 p(c₀|w)分别可以转换成计算 p(w|c₁)p(c₁)/p(w) 和 p(w|c₂)p(c₂)/p(w)。

由于分母部分都是p(w)，去掉分母部分，只计算比较分子部分 p(w|c₁)p(c₁) 和 p(w|c₂)p(c₂)。

而词向量w中有很多单词，为了降低计算难度，通常会认为这些词相互独立。

在概率计算中，独立事件的概率可以拆分单独计算。即

   p(w|c_i) p(c_i)

= p(w₁, w₂, ..., w_n|c_i) p(c_i)

= p(w₁|c_i) p(w₂|c_i) ... p(w_n|c_i) p(c_i)

那 p(w_n|c_i) 如何计算？这里需要画图说明。

假设非侮辱性的句子有两条。对应分别是['A', 'B'] 和 ['A', 'D']；

假设侮辱性的句子有三条。对应分别是['A', 'C']、['C', 'B'] 和 ['C', 'D']。

一共4个单词，组成一个词汇表['A', 'B', 'C', 'D']。

那么，根据非侮辱性句子得到词向量为[1, 1, 0, 0] 和 [1, 0, 0, 1]，如下图：

我们可以进一步统计对应单词在非侮辱性的情况下对应的个数。

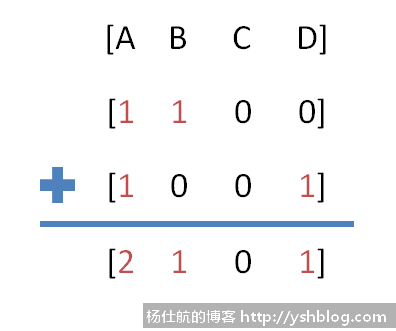
非侮辱性的情况，有2个A、1个B、0个C、1个D，共4个单词。

那么在已知非侮辱性的情况下(这是条件)，ABCD4个单词对应概率是对应个数除以该情况的单词总数。

ABCD4个单词对应条件概率为 [2/4, 1/4, 0/4, 1/4] = [0.5, 0.25, 0, 0.25]。

此处若想不通，就结合上篇博文朴素贝叶斯的理论知识的例子。把单词想成球，把条件想成桶。

在非侮辱性的桶里面，放着2个A球、1个B球和1个D球，没有C球。

已知从该桶任意取1个球是A球的概率为 2/4 = 0.5。

同理，对应侮辱性情况下的ABCD4个单词的条件概率为[1/6, 1/6, 3/6, 1/6]。

侮辱性情况有3个句子['A', 'C']、['C', 'B'] 和 ['C', 'D']，共1个A、1个B、3个C和1个D。

总结求得词汇表中每个单词的条件概率方法是在对应类别下，该单词的个数除以该类别的单词总数。

但这个条件概率不是我们要给正在归类的句子各个单词的条件概率。

这个简单，假如我们要判断句子['A', 'B', 'D']是什么属于类别。该句子包含3个单词A、B和D。

我们可以从刚才计算得到每种情况每个单词的条件概率中，获取对应单词的概率即可。

相当于我们从非侮辱性桶取出这3个球组成ABD句子，所以所需的条件概率计算方法一样，无须重复计算。

顺便把这个例子讲完，再写代码。

那么该句子属于非侮辱性的概率为：

    p(w|c₀) p(c₀)

= p('A'|c₀) p('B'|c₀) p('D'|c₀) p(c₀)

= 0.5*0.25*0.25*(2/5)

= 0.0125

这里的p(c₀)是非侮辱性的概率。训练集一共有5个句子，其中非侮辱性的句子2个，所以概率为2/5。

同理该句子属于侮辱性的概率为：

    p(w|c₁) p(c₁)

= p('A'|c₁) p('B'|c₁) p('D'|c₁) p(c₁)

= 1/6*1/6*1/6*(3/5)

≈ 0.0028

对比发现句子'ABD'属于非侮辱性的概率要大于属于侮辱性的概率。则句子'ABD'属于非侮辱性句子。

ps：这里我故意没有选择单词C组成句子，因为单词C在非侮辱性的情况概率为0。计算概率过程中乘以0会导致结果也为0。而且细心的同学会发现通常计算概率的结果都是小数点后好几位。这些情况下面代码会调整处理。

4、计算条件概率代码

上面通过简单例子讲解为什么以及如何计算条件概率，下面写代码实现。

《机器学习实战》书中的代码比较乱，且不通用。我重新整理如下：

#训练函数
def train_nb0(posting_vects, train_classes):
    num_train_docs = len(posting_vects) #总句子数
    num_words = len(posting_vects[0])   #词汇表单词数

    #遍历分类标签，统计对应类别的数量
    p_class_num = {} #各类别句子数
    p_vect_num = {}  #各类别各单词数
    
    for i, class_type in enumerate(train_classes):
        #累计每个类别的单词数（初始化每个类别单词数为1个，避免为0的情况）
        p_vect_num[class_type] = p_vect_num.get(class_type, np.ones(num_words)) + posting_vects[i]

        #累计每个类别的句子数
        p_class_num[class_type] = p_class_num.get(class_type, 0) + 1

    #计算每个类别的条件概率，对应单词数除以该类别的单词总数
    p_class = {} #各类别的概率
    p_vect = {}  #各类别的各单词条件概率

    for class_type in train_classes:
        p_vect[class_type] = p_vect_num[class_type]/np.sum(p_vect_num[class_type])
        p_class[class_type] = p_class_num[class_type]/float(num_train_docs)
    return p_vect, p_class

其中，注意以下几点：

1）参数postring_vects是训练集的6个句子数字化组合的列表；参数train_classes是每个句子对应分类的列表。

2）第12行，统计每个类别的单词数时，初始化为1

这是得到对应条件概率和各类别的概率。使用方法如下：

if __name__ == '__main__':
    #创建训练集
    posting_list, class_vect = create_dataset()

    #获取词汇表
    vocab_list = create_vocab_list(posting_list)

    #句子单词数字化
    posting_vects = []
    for posting in posting_list:
        posting_vect = set_of_words_to_vect(vocab_list, posting)
        posting_vects.append(posting_vect)

    #获取对应类别各单词的条件概率和各类别概率
    p_vect, p_class = train_nb0(np.array(posting_vects), np.array(class_vect))
    
    print(p_vect)
    print(p_class)

输出结果如下图：

5、朴素贝叶斯分类函数

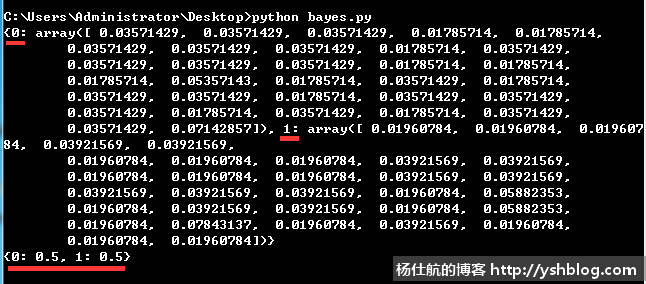
得到相应的条件概率之后，可以进行分类计算。继续添加如下方法：

#朴素贝叶斯分类函数
def classify_nb(vect_classify, p_vect, p_class):
    #计算句子属于各类别的概率
    p = {}
    for class_type, vect in p_vect.items():
        p[class_type] = np.sum(vect_classify * np.log(vect)) + np.log(p_class[class_type])

    #获取最大概率的类别
    return max(p.items(), key=lambda x:x[1])

这里为了方便运算，利用log的特性将乘法改成加法运算。这个知识自行查找即可。

vect_classify是一个句子数字化之后的词向量。只有两种值0和1，直接乘以条件概率可以保留对应单词的条件概率。去掉不相干单词的条件概率。

该方法使用如下，将完整的流程封装成一个方法，传递一个句子即可。

def testing_nb(test):
    #创建训练集
    posting_list, class_vect = create_dataset()

    #获取词汇表
    vocab_list = create_vocab_list(posting_list)

    #句子单词数字化
    posting_vects = []
    for posting in posting_list:
        posting_vect = set_of_words_to_vect(vocab_list, posting)
        posting_vects.append(posting_vect)

    p_vect, p_class = train_nb0(np.array(posting_vects), np.array(class_vect))
    
    #测试句子
    test_list = test.split(' ')
    vect_test = set_of_words_to_vect(vocab_list, test_list)
    return classify_nb(vect_test, p_vect, p_class)

测试如下：

if __name__ == '__main__':
    print(testing_nb('love my dalmation'))
    print(testing_nb('stupid garbage'))

结果如下：

第1个句子，归类为0，即非侮辱性；

第2个句子，归类为1，即是侮辱性。

《机器学习实战》相关的代码：

https://github.com/pbharrin/machinelearninginaction/blob/master/Ch04/bayes.py

我的完整代码：

#coding:utf-8
import numpy as np

#创建训练集
def create_dataset():
    posting_list = [
        'my dog has flea problems help please',
        'maybe not take him to dog park stupid',
        'my dalmation is so cute I love him',
        'stop posting stupid worthless garbage',
        'mr licks ate my steak how to stop him',
        'quit huying worthless dog food stupid'
    ]
    posting_list = map(lambda x:x.split(' '), posting_list)

    #上面句子对应的性质，0代表非侮辱性句子，1代表侮辱性句子
    class_vect = [0, 1, 0, 1, 0, 1]
    return posting_list, class_vect
    
#根据训练集生成词汇表
def create_vocab_list(posting_list):
    '''对所有句子取并集，获取词汇表'''
    return list(reduce(lambda x,y:x|set(y), [set([])] + posting_list))
    
#句子向量化
def set_of_words_to_vect(vocab_list, input_set):
    '''对比句子向量和词汇表，找到对应出现在词汇表的位置'''
    return map(lambda x: 1 if x in input_set else 0, vocab_list)
    
#训练函数
def train_nb0(posting_vects, train_classes):
    num_train_docs = len(posting_vects) #总句子数
    num_words = len(posting_vects[0])   #词汇表单词数

    #遍历分类标签，统计对应类别的数量
    p_class_num = {} #各类别句子数
    p_vect_num = {}  #各类别各单词数
    
    for i, class_type in enumerate(train_classes):
        #累计每个类别的单词数（初始化每个类别单词数为1个，避免为0的情况）
        p_vect_num[class_type] = p_vect_num.get(class_type, np.ones(num_words)) + posting_vects[i]

        #累计每个类别的句子数
        p_class_num[class_type] = p_class_num.get(class_type, 0) + 1

    #计算每个类别的条件概率，对应单词数除以该类别的单词总数
    p_class = {} #各类别的概率
    p_vect = {}  #各类别的各单词条件概率

    for class_type in train_classes:
        p_vect[class_type] = p_vect_num[class_type]/np.sum(p_vect_num[class_type])
        p_class[class_type] = p_class_num[class_type]/float(num_train_docs)
    return p_vect, p_class
    
#朴素贝叶斯分类函数
def classify_nb(vect_classify, p_vect, p_class):
    #计算句子属于各类别的概率
    p = {}
    for class_type, vect in p_vect.items():
        p[class_type] = np.sum(vect_classify * np.log(vect)) + np.log(p_class[class_type])

    #获取最大概率的类别
    return max(p.items(), key=lambda x:x[1])
    
def testing_nb(test):
    #创建训练集
    posting_list, class_vect = create_dataset()

    #获取词汇表
    vocab_list = create_vocab_list(posting_list)

    #句子单词数字化
    posting_vects = []
    for posting in posting_list:
        posting_vect = set_of_words_to_vect(vocab_list, posting)
        posting_vects.append(posting_vect)

    p_vect, p_class = train_nb0(np.array(posting_vects), np.array(class_vect))
    
    #测试句子
    test_list = test.split(' ')
    vect_test = set_of_words_to_vect(vocab_list, test_list)
    return classify_nb(vect_test, p_vect, p_class)
    
if __name__ == '__main__':
    print(testing_nb('love my dalmation'))
    print(testing_nb('stupid garbage'))

点击查看相关目录。

上一篇：机器学习08：朴素贝叶斯应用(词袋模式)

下一篇：机器学习06：朴素贝叶斯理论知识

相关专题： 机器学习实战