这段时间忙于弄其他事，有一段时间没学习机器学习。捡起来继续。

《机器学习实战》在决策树之后，讲基于概率论的分类方法：朴素贝叶斯。

前面讲的算法基本都是针对问题给出明确答案。但有些模糊的分类难以明确，这时候可以用概率论的方法来猜测一个较优的结果。概率论是许多机器学习方法的基础，而“朴素贝叶斯”是最简单的概率分类算法。

我们可以通过该算法了解概率论分类算法。

朴素贝叶斯是基于贝叶斯决策理论，学习该算法之前需要了解该理论。

如书中的示例，已知两个参数p1和p2的概率分布。

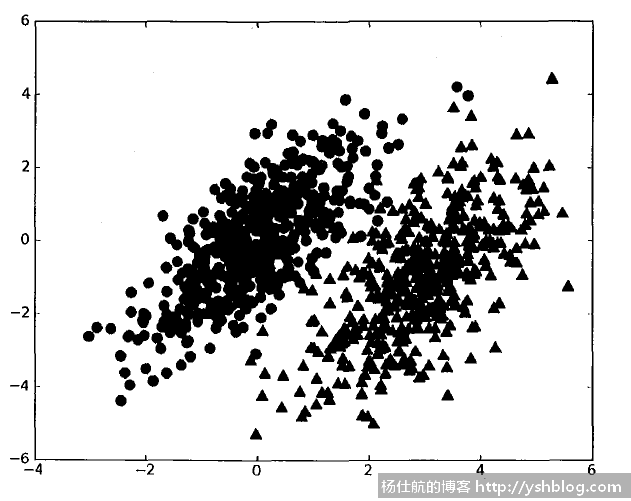
对于新的数据点(x, y)，分别计算两个参数的概率值 p1(x, y) 和 p2(x, y)。

若p1(x, y) > p2(x, y)，那么(x, y)属于p1类别。

若p2(x, y) > p1(x, y)，那么(x, y)属于p2类别。

新的数据点，我们选择高概率对应的类别作为该数据点的类别。

原理很清晰，重点是我们怎么得到p1和p2的概率分布，以及如何计算(x, y)的概率。

以上提到的p1()和p2()是简化描述。实际计算的时候，需要采用条件概率。

相关条件概率知识可以看《机器学习实战》中的第55-56页。

以下内容也是来自书中，但可能因为翻译原因，较难阅读和理解。故将其整理一下。

现有一个桶放了7个球，3个白球和4个黑球。

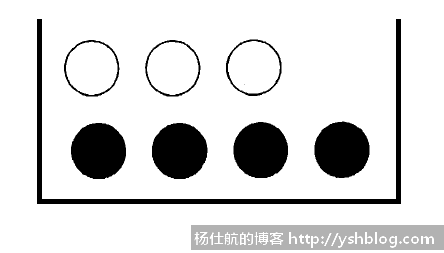
那么，随机取一个球，取得白球的概率为3/7，取得黑球的概率为4/7。

这里毫无疑问。稍微变化一下，将7个球分别装到两个桶里面。

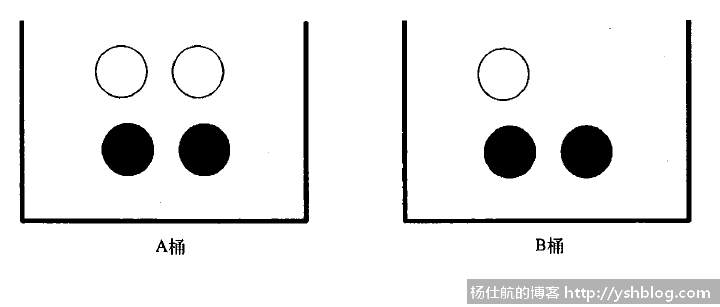
若随机从这两个桶中取一个球，取得白球的概率还是3/7。因为我们这时不考虑白球来自哪个桶。

若考虑白球来自哪个桶，即从B桶取得白球的概率应该是多少？

这个不难得到，B桶一共3个球，白球就1个。即概率为1/3。这个概率设定了条件，限制白球的来源，该概率称之为条件概率。

一般用p(白球|B桶)表示，即在B桶条件下，取得白球。

但有时候很难直接计算p(白球|B桶)的概率。可以用前人总结出来的条件概率公式计算。

p(白球|B桶) = p(白球 和 B桶)/p(白球)

p(白球 和 B桶) 是在A、B桶两个桶中取得白球，且白球来自B桶的概率。B同只有1个白球，两个桶共7个球，概率为1/7。

p(白球) 是在A、B桶取得白球的概率，不管白球来源，概率为3/7。

(1/7) / (3/7) = 1/3

以上是条件概率的知识。

实际应用到朴素贝叶斯上的条件概率要复杂一些。

上面提到对于新的数据点(x, y)，分别计算两个参数的概率值 p1(x, y) 和 p2(x, y)。

若p1(x, y) > p2(x, y)，那么(x, y)属于p1类别。

若p2(x, y) > p1(x, y)，那么(x, y)属于p2类别。

其中p1(), p2()是简化描述的结果。真正需要计算的是 p(c₁|x, y) 和 p(c₂|x, y)。

看起来很别扭？是的。我们把数据点(x, y)用w表示。即需要计算 p(c₁|w) 和 p(c₂|w)。

表示对于新数据w，p(c₁|w) 是c₁类别在w下的条件概率；p(c₂|w) 是c₂类别在w下的条件概率。

看这两个概率那个比较大，就说明w应该属于哪个类别。

当然，这个概率比较难计算。通常使用如下的“贝叶斯准则”交换条件和结果，进行求解。

这个为什么该算法叫做朴素贝叶斯的重要原因。具体用法，下篇博文找个实例讲解。

点击查看相关目录。

上一篇：机器学习07：朴素贝叶斯应用(词集模式)

下一篇：If函数及Excel公式入门

相关专题： 机器学习实战