Python秒解最难数独

  • 发布时间：2016年9月29日 17:41
  • 作者：杨仕航
  • 分类标签： Python
  • 阅读(41898)
  • 评论(2)

最近在学机器学习，其中numpy是必学的库。学习过程中，产生一个想法：用numpy解数独，锻炼numpy的用法。

查了一下程序解数独有暴力破解和Dancing Links等方法。感觉还是太慢了。自己写一个算法求解数独。

讲算法的东西，文章篇幅会很长，请做好心理准备。算法我命名为排除候选猜测法。完整的代码在文章底部，不想看过程可以直接跳到最尾处。


numpy可以创建多维的数组，并且可以快速得到对应行、列和九宫格的位置。那么我可以创建1个9*9的二维数组。

若其中某个坐标的值是确定的，则用数字填入；未确定下来，则用一个list列表，列表中是可能的值作为候选。拿一个简单的数独举例，如下：

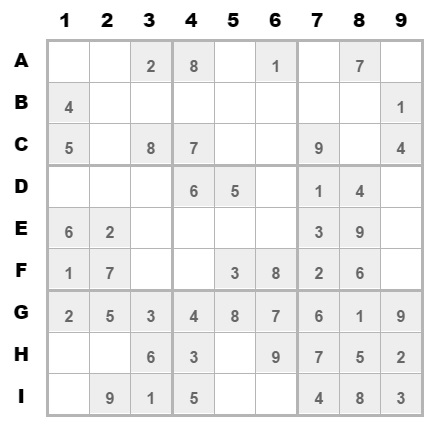
这是1个9*9的二维数组，确定的数字直接填到对应的坐标上。没填上数字的坐标可能候选值是1~9，再根据确定的值排除候选值，如下结果：

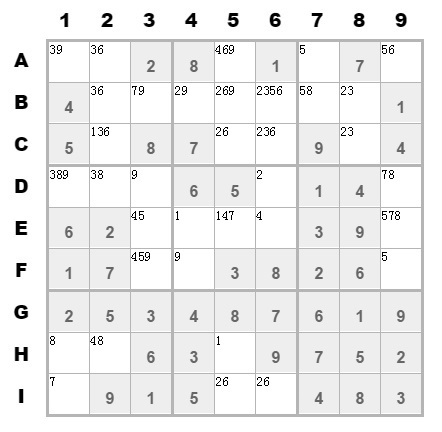
接着利用数独的规则，一步一步排除候选值，直到候选值剩下1个为止。（这是我的算法中前半部分，大部分数独题目用该部分的逻辑就可以解出来了）

故，该算法先称为排除候选法。(加上后半部分的算法再改名)


创建一个类，初始化数据：

#coding:utf-8
#python2.7
#Create:   2016-09-27
#Complete: 2016-09-29
__author__ = u"杨仕航"

import numpy as np
from Queue import Queue, LifoQueue

class Sudo():
    def __init__(self, data):
        #数据初始化(二维的object数组，值可填数字和list)
        self.value = np.array([[0]*9]*9, dtype=object)
        self.new_points = Queue()  #先进先出的新解坐标
        
        #后半部分算法需要的属性
        self.recoder = LifoQueue() #先进后出的回溯器
        self.guess_times = 0       #猜测次数
        
        #九宫格的基准列表
        self.base_points=[[0,0],[0,3],[0,6],[3,0],[3,3],[3,6],[6,0],[6,3],[6,6]]
        
        #整理数据
        #将81个元素的list转化为9*9的二维数组
        data = np.array(data).reshape(9,-1)
        for r in range(0,9):
            for c in range(0,9):
                if data[r,c]:
                    self.value[r,c] = data[r,c]
                    #新点添加到列表中，以便遍历
                    self.new_points.put((r,c))
                else:
                    self.value[r,c] = [1,2,3,4,5,6,7,8,9]

若没有numpy库，就安装。另外Queue是列队(栈)，先进先出。每新增一个确定的数字，则加入这个列队。后续处理则从这个列队取出数字，排除所在行列和九宫格其他候选值。

剔除候选值的方法如下（该方法在这个类中）： 

    #剔除数字
    def _cut_num(self, point):
        r, c = point
        val = self.value[r, c]

        #行
        for i, item in enumerate(self.value[r]):
            if isinstance(item, list):
                if item.count(val):
                    item.remove(val)

                    #判断移除后，是否剩下一个元素
                    if len(item)==1:
                        self.new_points.put((r, i))
                        self.value[r,i] = item[0]

        #列
        for i, item in enumerate(self.value[:,c]):
            if isinstance(item, list):
                if item.count(val):
                    item.remove(val)

                    #判断移除后，是否剩下一个元素
                    if len(item)==1:
                        self.new_points.put((i, c))
                        self.value[i,c] = item[0]

        #所在九宫格(3x3的数组)
        b_r, b_c = map(lambda x:x/3*3, point) #九宫格基准点
        for m_r, row in enumerate(self.value[b_r:b_r+3, b_c:b_c+3]):
            for m_c, item in enumerate(row):
                if isinstance(item, list):
                    if item.count(val):
                        item.remove(val)

                        #判断移除后，是否剩下一个元素
                        if len(item)==1:
                            r = b_r + m_r
                            c = b_c + m_c
                            self.new_points.put((r, c))
                            self.value[r,c]=item[0]

传入坐标值，根据数独的规则：同行、同列和同个九宫格内不能填写同样的数字。遍历所在的行列、九宫格，去掉相同的候选值。

好吧，单单看代码有点复杂。简单画几个图解释一下：


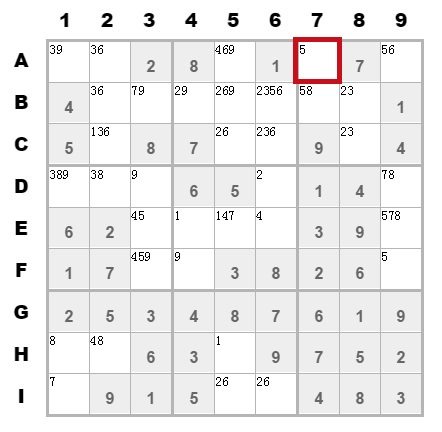
这是刚才上面的图，可以确定A7单元格要填数字5。那么接下来需要把A7所在的第A行和第7列以及该九宫格上候选值有5的话，去除掉。

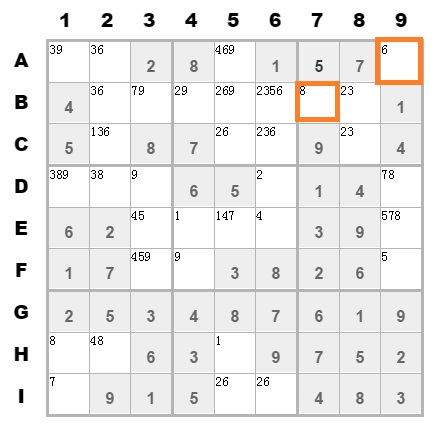
这样就去掉B7单元格和A9单元格上的候选值5，剩下1个数字。

剩下1个数字之后，就可以确定该单元格的数字。再循环上面的步骤。


只是剔除候选值一种方法还不够。有时候存在如下情况：

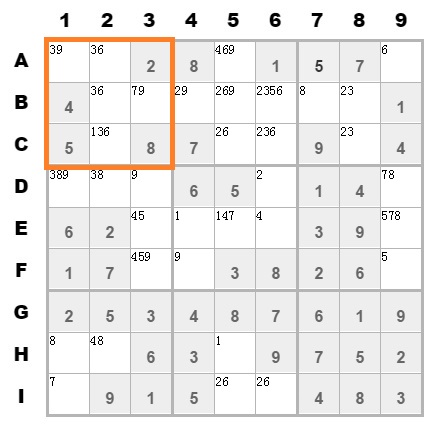
在第1个九宫格中，有4个单元格是确定了；有6个单元格未确定。其中B7单元格比较特殊，该单元格候选值[7,9]中的7在该九宫格是唯一存在的。

这意味在该九宫格中，其他单元格不可能填7，只有这个单元格才可以填7。所以可以确定该单元格的数字了。

同样道理，同一行和同一列也可以这样判断。判断代码如下： 

    #同一行、列或九宫格中1~9可能性只有一个的情况
    def _check_one_possbile(self):
        #同一行只有一个数字的情况
        for r in range(0,9):
            values = filter(lambda x:isinstance(x,list), self.value[r])

            for c, item in enumerate(self.value[r]):
                if isinstance(item, list):
                    for value in item:
                        if sum(map(lambda x:x.count(value), values)) == 1:
                            self.value[r,c] = value
                            self.new_points.put((r,c))
                            return True

        #同一列只有一个数字的情况
        for c in range(0,9):
            values = filter(lambda x:isinstance(x,list), self.value[:,c])

            for r, item in enumerate(self.value[:,c]):
                if isinstance(item, list):
                    for value in item:
                        if sum(map(lambda x:x.count(value), values)) == 1:
                            self.value[r,c] = value
                            self.new_points.put((r,c))
                            return True

        #九宫格内的单元格只有一个数字的情况
        for r,c in self.base_points:
            values = filter(lambda x:isinstance(x,list), self.value[r:r+3,c:c+3].reshape(1,-1)[0])

            for m_r, row in enumerate(self.value[r:r+3,c:c+3]):
                for m_c, item in enumerate(row):
                    if isinstance(item, list):            
                        for value in item:
                            if sum(map(lambda x:x.count(value), values)) == 1:
                                self.value[r+m_r, c+m_c] = value
                                self.new_points.put((r+m_r, c+m_c))
                                return True

这里有个小细节，是我写这个算法的时候，后期调整的。当每找到唯一确定的值之后，添加到列表就返回True并跳出该方法。为了确保可以及时处理确定的值，排除其他候选值。避免判断出错。


去掉候选值，除了以上的方法之外。我还写了一个方法。同行列隐性排除，这个名称有点难理解。看图(该图的数据是模拟的)：

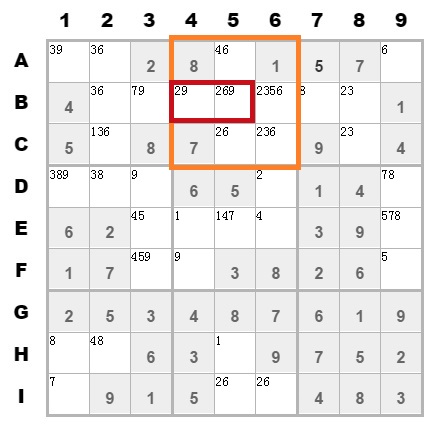
在第二个九宫格中，候选值数字9只存在B4和B5单元格中。虽然我不确定9到底填在哪个单元格中，但我可以确定。第B行的数字9一定出现在这两个单元格中。则第B行除了第2个九宫格所在的列，其他该行的位置可以排除掉9。

即排除掉B3单元格上的9。

这个要熟悉掌握数独的规则就可以理解这种做法的原理。代码也可以实现，如下： 

    #同一个九宫格内数字在同一行或同一列处理
    def _check_same_num(self):
        for b_r, b_c in self.base_points:
            block = self.value[b_r:b_r+3,b_c:b_c+3]

            #判断数字1~9在该九宫格的分布情况
            data = block.reshape(1,-1)[0]
            for i in range(1,10):
                result = map(lambda x: 0 if not isinstance(x[1], list) else x[0]+1 if x[1].count(i) else 0, enumerate(data))
                result = filter(lambda x:x>0,result)
                r_count = len(result)
 
                if r_count in [2, 3]:
                    #2或3个元素才有可能同一行或同一列
                    rows = map(lambda x:(x-1)/3, result)
                    cols = map(lambda x:(x-1)%3, result)

                    if len(set(rows)) == 1:
                        #同一行，去掉其他行的数字
                        result = map(lambda x: b_c + (x-1)%3, result)
                        row = b_r + rows[0]

                        for col in range(0,9):
                            if not col in result:
                                item = self.value[row, col]
                                if isinstance(item, list):
                                    if item.count(i):
                                        item.remove(i)

                                        #判断移除后，是否剩下一个元素
                                        if len(item)==1:
                                            self.new_points.put((row, col))
                                            self.value[row, col] = item[0]
                                            return True
                        
                    elif len(set(cols)) == 1:
                        #同一列
                        result = map(lambda x: b_r + (x-1)/3, result)
                        col = b_c + cols[0]
 
                        for row in range(0,9):
                            if not row in result:
                                item = self.value[row, col]
                                if isinstance(item, list):
                                    if item.count(i):
                                        item.remove(i)

                                        #判断移除后，是否剩下一个元素
                                        if len(item)==1:
                                            self.new_points.put((row, col))
                                            self.value[row, col] = item[0]
                                            return True

这里判断是否是同一行列，需要逐个遍历九宫格中的候选值，提取数字1~9所在的位置。

首先，我把九宫格的二维数组变成一维列表。这样九宫格的位置可以顺序化。

有顺序之后，我就可以判断这些数字的分布是否是同一行或同一列。这样也许看不出什么东西，再把这些序号一一对应到原来的九宫格上。如下图：

同一行的话，这些序号除以3之后的值相同；

同一列的话，这些序号除以3之后的余数相同。

细心一点的话，可以发现这里同样只要有确定的值，就返回True跳出方法。

我把3种方法都讲解完成，是时候亮剑了。算法前半部分的算法逻辑如下： 

    #排除法解题
    def solve_sudo(self):
        is_run_same = True
        is_run_one = True

        while is_run_same:
            while is_run_one:
                #剔除数字
                while not self.new_points.empty():
                    point = self.new_points.get() #先进先出
                    self._cut_num(point)

                #检查单个数字的情况
                is_run_one = self._check_one_possbile()

            #检查同行或列的情况
            is_run_same = self._check_same_num()
            is_run_one = True

_cut_num方法是可以完全肯定把数字确定下来。所以要不断处理，直到列队没有值为止。

另外两种方法一旦发现可以确定的值，就需要跳出。避免判断出错。

其实排除候选的方法不止这三种，还有其他方法。若你觉得可以提高算法效率的话，可以试试加入进来。

更多排除方法可以参考：琳琅在线。



现在开始说说后半部分的算法。

因为有时候，排除到最后，还可能有些值模棱两可，无法确定下来。这时候就需要猜了。

从候选值中挑出一个值确定下来，再用前半部分的算法处理。

前半部分处理完成之后，有两种情况：解答完成和未解答完成。

解答完成就是全部数字都确定下来了。可以用该方法得到确认下来的数字： 

    #得到有多少个确定的数字
    def get_num_count(self):
        return sum(map(lambda x: 1 if isinstance(x,int) else 0, self.value.reshape(1,-1)[0]))

因为确认下来的数字，填写的是数字。则只需统计int类型的个数即可。

若确定的数字不足9*9=81个的话，就说明未解答完成，还需要继续猜测。

不管解开和未解开，还需要对结果进行验证。毕竟这个结果是上一次猜测的结果。

验证方法如下： 

    #检查有没错误
    def check_value(self):
        #行
        for row in self.value:
            nums = []
            lists = []
            for item in row:
                (lists if isinstance(item,list) else nums).append(item)
            if len(set(nums)) != len(nums):
                return False #数字要不重复
            if len(filter(lambda x: len(x)==0, lists)):
                return False #候选列表不能为空集

        #列
        for c in range(0,9):
            nums = []
            lists = []
            col = self.value[:,c]
            
            for item in col:
                (lists if isinstance(item,list) else nums).append(item)
            if len(set(nums)) != len(nums):
                return False #数字要不重复
            if len(filter(lambda x: len(x)==0, lists)):
                return False #候选列表不能为空集

        #九宫格
        for b_r, b_c in self.base_points:
            nums = []
            lists = []
            block = self.value[b_r:b_r+3,b_c:b_c+3].reshape(1,-1)[0]

            for item in block:
                (lists if isinstance(item,list) else nums).append(item)
            if len(set(nums)) != len(nums):
                return False #数字要不重复
            if len(filter(lambda x: len(x)==0, lists)):
                return False #候选列表不能为空集
        return True


为了优化算法，进行猜测的位置也不是随便挑选的。

候选列表的数字越少越有利。so~ 可以对每个候选列表评分，取最高分的即可： 

    #评分，找到最佳的猜测坐标
    def get_best_point(self):
        best_score = 0
        best_point = (0,0)

        for r, row in enumerate(self.value):
            for c, item in enumerate(row):
                point_score = self._get_point_score((r,c))
                if best_score < point_score:
                    best_score = point_score
                    best_point = (r,c)
        return best_point

    #计算某坐标的评分
    def _get_point_score(self, point):
        #评分标准 (10-候选个数) + 同行确定数字个数 + 同列确实数字个数
        r,c = point
        item = self.value[r,c]

        if isinstance(item, list):
            score = 10 - len(item)
            score += sum(map(lambda x: 1 if isinstance(x,int) else 0, self.value[r]))
            score += sum(map(lambda x: 1 if isinstance(x,int) else 0, self.value[:,c]))
            return score
        else:
            return 0


后半部分的逻辑理顺了，该算法完整的名称，命名为排除候选猜测法。

猜测就需要回溯，所以要引入“堆”先进后出。 

from Queue import LifoQueue

涉及到对象的复制，要需要深度拷贝。numpy也有拷贝，不过还是会有影响。 

import copy

另外，回溯需要保存的数据比较多。我创建一个类专门用于保存相应的数据：

class Recoder():
    point = None        #进行猜测的点所在坐标
    point_index = 0     #猜测候选列表使用的值的索引
    value = None        #回溯记录的9*9数组

猜测的算法如下(同样写在Sudo类之中)：

    #猜测记录
    def recode_guess(self, point, index=0):
        #记录
        recoder = Recoder()
        recoder.point = point
        recoder.point_index = index
        #recoder.value = self.value.copy() #numpy的copy不行
        recoder.value = copy.deepcopy(self.value)
        self.recoder.put(recoder)
        self.guess_times += 1 #记录猜测次数

        #新一轮的排除处理
        item = self.value[point]
        self.value[point] = item[index]
        self.new_points.put(point)
        self.solve_sudo()

    #回溯，需要先进后出
    def reback(self):
        while True:
            if self.recoder.empty():
                raise Exception('sudo is wrong')
            else:
                recoder = self.recoder.get()
                point = recoder.point
                index = recoder.point_index + 1
                item = recoder.value[point]

                #判断索引是否超出范围。若超出，则再回溯一次
                if index < len(item):
                    break

        self.value = recoder.value
        self.recode_guess(point, index)

    #解题
    def calc(self):
        #第一次解题  
        self.solve_sudo()

        #检查有没错误的，有错误的则回溯；没错误却未解开题目，则再猜测
        while True:
            if self.check_value():
                if self.get_num_count() == 81:
                    break
                else:
                    #获取最佳猜测点
                    point = self.get_best_point()
                    
                    #记录并处理
                    self.recode_guess(point)            
            else:
                #出错，则回溯，尝试下一个猜测
                self.reback()

这里再稍微讲解一下猜测-回溯的逻辑，举例说明。执行calc方法：

假如B3单元格候选列表[2,9]。

第1次：猜测B3第1个值，值为2；

排除候选计算之后，发现还未完成。继续猜测，选中D5，候选为[3，7]；

第2次：猜测D5第1个值，值为3；

排除候选计算之后，发现有误。需要回溯到未猜测D5第1个值之前的状态。重新猜测；

第3次：发现D5还有第2个值未猜测，猜测D5第2个值，值为7；

排除候选计算之后，发现有误。需要回溯到未猜测D5第2个值之前的状态。重新猜测；

发现D5已经没有值可以猜测了，继续回溯。

回溯到猜测B3第1个值的状态，发现D5还有第2个值未猜测；

第4次：猜测B3第2个值，值为9。

...

这样一直下去，直到解答题目为止。


算法完成了，拿一些数独题目测试一下。数独题目大部分来自http://cn.sudokupuzzle.org/ 

if __name__ == '__main__':
    #数独题目来源 http://cn.sudokupuzzle.org/
    #需要测试哪个就保留哪个
    #2016-09-27 入门
    data = [0,0,2, 8,0,1, 0,7,0,
            4,0,0, 0,0,0, 0,0,1,
            5,0,8, 7,0,0, 9,0,4,
            0,0,0, 6,5,0, 1,4,0,
            6,2,0, 0,0,0, 3,9,0,
            1,7,0, 0,3,8, 2,6,0,
            2,5,3, 4,8,7, 6,1,9,
            0,0,6, 3,0,9, 7,5,2,
            0,9,1, 5,0,0, 4,8,3]

    #2016-09-27 初级
    data = [0,0,0, 0,0,0, 0,0,0,
            0,6,0, 3,0,4, 0,2,0,
            0,0,0, 0,0,0, 0,7,5,
            0,0,0, 0,0,0, 0,0,0,
            0,0,0, 6,8,0, 3,0,0,
            1,0,5, 0,7,0, 0,0,0,
            0,0,0, 0,5,0, 0,0,0,
            0,3,0, 0,0,0, 4,0,0,
            8,0,0, 9,0,0, 0,0,0]

    #2016-09-26 中级
    data = [0,0,0, 0,0,0, 0,5,9,
            0,1,0, 0,0,4, 0,0,0,
            0,8,0, 1,0,0, 0,0,0,
            0,0,0, 0,0,0, 4,0,7,
            5,0,3, 0,6,0, 0,0,0,
            9,0,0, 0,0,0, 0,0,0,
            6,0,0, 0,0,0, 0,3,0,
            0,0,0, 0,0,1, 0,0,0,
            0,7,0, 8,0,0, 2,0,0]

    #2016-09-30 高级
    data = [0,8,0, 0,0,0, 0,0,0,
            9,0,0, 5,0,0, 7,0,0,
            0,0,1, 0,0,4, 0,0,2,
            8,0,0, 0,0,1, 2,0,4,
            0,0,0, 0,9,0, 0,0,0,
            0,5,3, 7,0,0, 0,9,0,
            0,6,0, 0,0,2, 0,8,0,
            0,0,2, 1,0,0, 0,0,7,
            0,0,0, 0,0,0, 6,0,0]

    #号称最难的数独
    data = [8,0,0, 0,0,0, 0,0,0,
            0,0,3, 6,0,0, 0,0,0,
            0,7,0, 0,9,0, 2,0,0,
            0,5,0, 0,0,7, 0,0,0,
            0,0,0, 0,4,5, 7,0,0,
            0,0,0, 1,0,0, 0,3,0,
            0,0,1, 0,0,0, 0,6,8,
            0,0,8, 5,0,0, 0,1,0,
            0,9,0, 0,0,0, 4,0,0]

    try:
        t1 = time.time()
        sudo = Sudo(data)
        sudo.calc()
        t2=time.time()

        print(u"完成，猜测了%s次" % sudo.guess_times)
        print(sudo.value)
        print(u"耗时：%.3fs" % (t2-t1))

    except Exception as e:
        print(e)

上面题目用时如下，我的电脑CPU是i3，内存8G：

2016-09-27 入门：0.004s，猜测0次

2016-09-27 初级：0.013s，猜测0次

2016-09-26 中级：0.210s，猜测74次

2016-09-30 高级：0.034s，猜测9次

号称最难的数独：0.330s，猜测109次

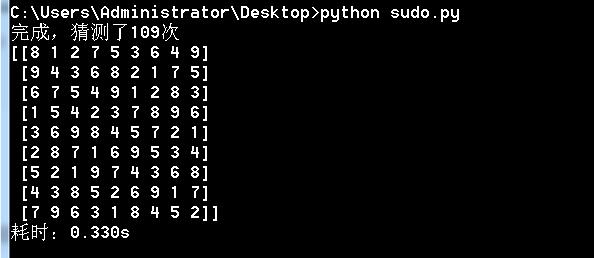
速度惊人，可见我这个算法效率还是可以的。

从上面的数据，可以发现：用时和猜测次数有关系，同时猜测次数也可以反应数独题目的难度。


完整代码如下(点击按钮)：

上一篇：VSTO新手常见问题

下一篇：vb/vba颜色和RGB颜色互转

相关专题： 我为数独迷   

评论列表

智慧如你，不想发表一下意见吗？

新的评论

清空

建议反馈

1、可在相应的博文底下评论

2、发邮件到2872402050@qq.com

Welcome to visit my website © Haddy Yang